【题目】为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.

(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
参考答案:
【答案】(1)、48;(2)、90°;(3)、300.
【解析】
试题分析:(1)、根据条形统计图求出总人数;(2)、根据音乐人数占总人数的比值求出圆心角的度数;(3)、根据样本中美术的比值求出总人数.
试题解析:(1)、12+16+6+10+4=48(人)
(2)、12÷48×360°=90°
(3)、6÷48×2400=300(人)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间共有28名工人生产螺栓和螺母,每人平均每天生产螺栓12个或螺母18个,问:如何安排工人才能使每天生产的螺栓和螺母按1:2配套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为治理大气污染,保护人民健康.某市积极行动,调整产业结构,压减钢铁生产总量,2013年某市钢铁生产量为9700万吨,计划到2015年钢铁生产量设定为5000万吨,设该市每年钢铁生产量平均降低率为x,依题意,下面所列方程正确的是( )
A. 9700(1﹣2x)=5000 B. 5000(1+x)2=9700
C. 5000(1﹣2x)=9700 D. 9700(1﹣x)2=5000
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是( )
A.x=2 B.x=4 C.x=8 D.x=10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为 .
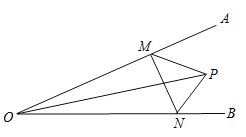
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C不在同一直线上,顺次连接AB、BC、CA.
(Ⅰ)如图①,点D在线段BC上,DE∥AB交AC于点E,∠EDF=∠A.求证:DF∥AC.
(Ⅱ)如图②,若点D在BC的延长线上,DE∥AB交AC的延长线于点E,DF∥AC交BA的延长线于点F.问∠EDF与∠BAC有怎样的关系,说明理由.
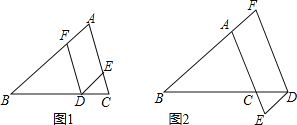
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图,请根据图中提供的信息,解答下面的问题:
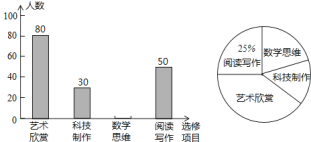
(1)此次共调查了______名学生,扇形统计图中“艺术鉴赏”部分的圆心角是______度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
相关试题

