【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1 , 并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2 , 使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
参考答案:
【答案】
(1)
如图,△A1B1C1即为所求,C1(2,﹣2)
(2)
如图,
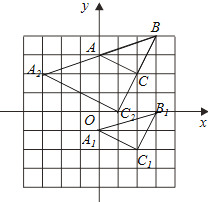
△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣ ![]() ×2×6﹣
×2×6﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×2×4
×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
【解析】(1)根据网格结构,找出点A、B、C向下平移4个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;(2)延长BA到A2 , 使AA2=AB,延长BC到C2 , 使CC2=BC,然后连接A2C2即可,再根据平面直角坐标系写出C2点的坐标,利用△A2BC2所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【考点精析】解答此题的关键在于理解作图-位似变换的相关知识,掌握对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在
 处,规定向北方向为正,当天行驶纪录如下(单位:千米)
处,规定向北方向为正,当天行驶纪录如下(单位:千米) ,
, ,
, ,
,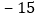 ,
, ,
, ,
, ,
,
 在岗亭何方?距岗亭多远?
在岗亭何方?距岗亭多远? 在行驶过程中,最远处离出发点有多远?
在行驶过程中,最远处离出发点有多远?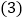 若摩托车行驶
若摩托车行驶 千米耗油
千米耗油 升,这一天共耗油多少升?
升,这一天共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有
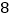 箱桔子,以每箱
箱桔子,以每箱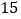 千克为标准,称重记录如下(单位:千克,超过标准的千克数为正数,不足标准的千克数记为负数):
千克为标准,称重记录如下(单位:千克,超过标准的千克数为正数,不足标准的千克数记为负数):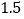 ,
,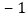 ,
,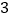 ,
,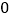 ,
,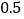 ,
,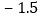 ,
,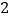 ,
,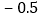 .
.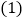 称得的
称得的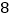 箱总质量与标准总质量相比超过或不足多少千克?
箱总质量与标准总质量相比超过或不足多少千克?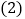 若每箱桔子进价
若每箱桔子进价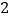 元/千克,售价
元/千克,售价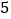 元/千克,则这
元/千克,则这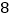 箱桔子全部售出共盈利多少钱?
箱桔子全部售出共盈利多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若
 ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小型企业实行工资与业绩挂钩制度,工人工资分为A、B、C、D四个档次.小明对该企业三月份工人工资进行调查,并根据收集到的数据,绘制了如下尚不完整的统计表与扇形统计图.


根据上面提供的信息,回答下列问题:
(1)求该企业共有多少人?
(2)请将统计表补充完整;
(3)扇形统计图中“C档次”的扇形所对的圆心角是度. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得元购物券,至多可得元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
相关试题

