【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果,(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
参考答案:
【答案】
(1)解:画树状图如下:

则共有12种等可能的结果数
(2)解:∵共有12种等可能的结果数,抽到的两张卡片上的数都是勾股数的结果数为6种,
∴抽到的两张卡片上的数都是勾股数的概率= ![]() =
= ![]()
【解析】(1)抓住已知,现从中随机抽取一张,不放回,然后就出树状图,一共有12种可能。
(2)观察卡片上的数字,可知卡片A上的三个数不是勾股数,因此满足条件的结果数只有6种,根据概率公式即可求解。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中有大小不同的平行四边形,第一幅图中有1个平行四边形,第二幅图中有3个平行四边形,第三幅图中有5个平行四边形,则第6幅和第7幅图中合计有( )个平行四边形

A.22B.24C.26D.28
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
第1个等式:a1=
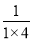 =
=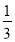 ×(
×(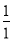 ﹣
﹣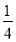 );
);第2个等式:a2=
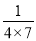 =
=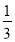 ×(
×(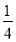 ﹣
﹣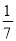 );
);第3个等式:a3=
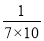 =
=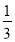 ×(
×(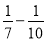 );
);第4个等式:a4=
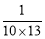 =
=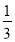 ×(
×(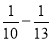 );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a100的值;
(3)数学符号
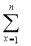 f(x)=f(1)+f(2)+f(3)+…+f(n),试求
f(x)=f(1)+f(2)+f(3)+…+f(n),试求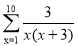 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车一天上午从A地出发在沿着东西向的大街营运,向东为正,向西为负,行驶里程(单位:km)依先后次序记录如下:+18,-5,-2,+3,+10,-9,+12,-3,-7,-15.(1)将最后一名乘客送到目的地,出租车相对出发地的位置?(2)不超过3千米时,按起步价收费10元,超过3千米的部分,每千米收费2元,司机上午的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=
 ;④S△AEF=
;④S△AEF= .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家住房户型呈长方形,平面图如下(单位:米).现准备铺设整个长方形地面,其中三间卧室铺设木地板,其它区域铺设地砖.(房间内隔墙宽度忽略不计)

(1)求a的值;
(2)请用含x的代数式分别表示铺设地面需要木地板和地砖各多少平方米;
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米.装修公司有A,B两种活动方案,如表:
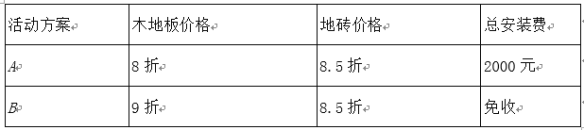
已知卧室2的面积为21平方米,则小方家应选择哪种活动,使铺设地面总费用(含材料费及安装费)更低?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,C,D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=2
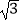 .
.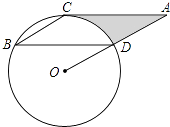
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
相关试题

