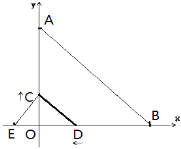
【题目】如图,已知点A(0,8)、B(8,0)、E(-2,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒2个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒。
(1)填空:直线AB的解析式是_____________________;
(2)求t的值,使得直线CD∥AB;
(3)是否存在时刻t,使得△ECD是等腰三角形?若存在,请求出一个这样的t值;若不存在,请说明理由。
参考答案:
【答案】![]()
【解析】(1)由点A、B的坐标,利用待定系数法求出直线解析式即可;
(2)当CD∥AB时,∠CDO=∠ABO,根据tan∠CDO=tan∠ABO列方程求解即可;
(3)当EO=DO时,△ECD是等腰三角形,从而可求出t的值.
(1)将点A(0,8)、B(8,0)代入y=kx+b中,
得:![]() ,解得:
,解得:![]() ,
,
∴该直线的解析式为y=-x+8.
故答案为:y=-x+8.
(2)当直线AB∥CD时,∠CDO=∠ABO,
∴tan∠CDO=tan∠ABO
∴![]() ,解得,
,解得,![]() .
.
故当![]() 时,AB∥CD.
时,AB∥CD.
(3)存在.事实上,当EO=OD时,△ECD就是等腰三角形,
此时,EO=2,OD=8-2t,
由![]() ,
,
解得,![]() .
.
∴存在时刻T,当![]() 时,△ECD是等腰三角形
时,△ECD是等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=kx+b(k<0)与函数y=
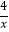 (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a,
(x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, 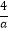 )、(c,
)、(c, 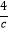 ),其中a>c>0.
),其中a>c>0.
(1)如图①,求证:∠EDP=∠ACP;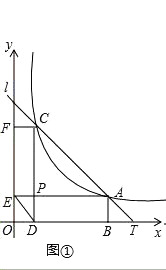
(2)如图②,若A、D、E、C四点在同一圆上,求k的值;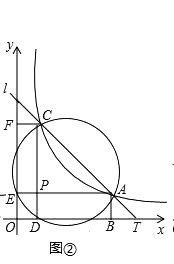
(3)如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.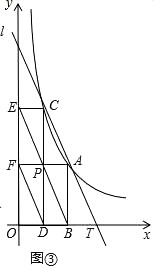
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距2400米,甲、乙两人分别从A,B两地同时出发相向而行,乙的速度是甲的2倍,已知乙到达A地15分钟后甲到达B地.
(1)求甲每分钟走多少米?
(2)两人出发多少分钟后恰好相距480米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:

(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:菱形的两条对角线互相垂直. 已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )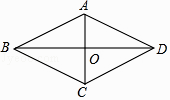
A.③→②→①→④
B.③→④→①→②
C.①→②→④→③
D.①→④→③→② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件正确的是( )
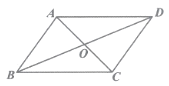
A. AB=AD B. AC=BD C. ∠ABC=90° D. ∠ABC=∠ADC
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
相关试题

