【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).

参考答案:
【答案】(1)AAS;(2)AB=4;(3)![]() .
.
【解析】
试题分析:(1)作AF⊥BC,根据已知条件易得∠AFB=∠BEA,∠DAB=∠ABD,AB=AB,根据AAS可判断出△ABF≌△BAE;(2)连接AD,作CG⊥AF,易得tan∠DAE=![]() ,再由tan∠F=tan∠DAE,求出CG,再证△DCG∽△ACE,根据相似三角形的性质即可求出AC;(3)过点D作DG⊥BC,设DG=a,在Rt△ABH,Rt△ADN,Rt△ABH中分别用a,k表示出AB=2a(k+1),BH=
,再由tan∠F=tan∠DAE,求出CG,再证△DCG∽△ACE,根据相似三角形的性质即可求出AC;(3)过点D作DG⊥BC,设DG=a,在Rt△ABH,Rt△ADN,Rt△ABH中分别用a,k表示出AB=2a(k+1),BH=![]() a(k+1),BC=2BH=2
a(k+1),BC=2BH=2![]() a(k+1),CG=
a(k+1),CG=![]() a(2k+1),DN=
a(2k+1),DN=![]() ka,最后用△NDE∽△GDC,求出AE,EC即可.
ka,最后用△NDE∽△GDC,求出AE,EC即可.
试题解析:证明:(1)如图2,
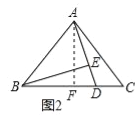
作AF⊥BC,
∵BE⊥AD,∴∠AFB=∠BEA,
在△ABF和△BAE中,
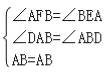 ,
,
∴△ABF≌△BAE(AAS),
∴BF=AE
∵AB=AC,AF⊥BC,
∴BF=![]() BC,
BC,
∴BC=2AE,
故答案为AAS
(2)如图3,
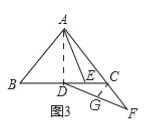
连接AD,作CG⊥AF,
在Rt△ABC中,AB=AC,点D是BC中点,
∴AD=CD,
∵点E是DC中点,
∴DE=![]() CD=
CD=![]() AD,
AD,
∴tan∠DAE=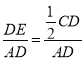 =
=![]() ,
,
∵AB=AC,∠BAC=90°,点D为BC中点,
∴∠ADC=90°,∠ACB=∠DAC=45°,
∴∠F+∠CDF=∠ACB=45°,
∵∠CDF=∠EAC,
∴∠F+∠EAC=45°,
∵∠DAE+∠EAC=45°,
∴∠F=∠DAE,
∴tan∠F=tan∠DAE=![]() ,
,
∴![]() ,
,
∴CG=![]() ×2=1,
×2=1,
∵∠ACG=90°,∠ACB=45°,
∴∠DCG=45°,
∵∠CDF=∠EAC,
∴△DCG∽△ACE,
∴![]() ,
,
∵CD=![]() AC,CE=
AC,CE=![]() CD=
CD=![]() AC,
AC,
∴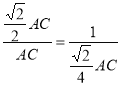 ,
,
∴AC=4;
∴AB=4;
(3)如图4,
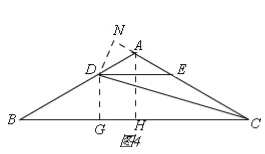
过点D作DG⊥BC,设DG=a,
在Rt△BGD中,∠B=30°,
∴BD=2a,BG=![]() a,
a,
∵AD=kDB,
∴AD=2ka,AB=BD+AD=2a+2ka=2a(k+1),
过点A作AH⊥BC,
在Rt△ABH中,∠B=30°.
∴BH=![]() a(k+1),
a(k+1),
∵AB=AC,AH⊥BC,
∴BC=2BH=2![]() a(k+1),
a(k+1),
∴CG=BC﹣BG=![]() a(2k+1),
a(2k+1),
过D作DN⊥AC交CA延长线与N,
∵∠BAC=120°,
∴∠DAN=60°,
∴∠ADN=30°,
∴AN=ka,DN=![]() ka,
ka,
∵∠DGC=∠AND=90°,∠AED=∠BCD,
∴△NDE∽△GDC.
∴![]() ,
,
∴![]() ,
,
∴NE=3ak(2k+1),
∴EC=AC﹣AE=AB﹣AE=2a(k+1)﹣2ak(3k+1)=2a(1﹣3k2),
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线m外有一定点A,A到直线m的距离是7 cm,B是直线m上的任意一点,则线段AB的长度:AB___________7 cm.(填写“<”“>”“=”“≤”或“≥”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形、直角三角形、等边三角形、长方形、圆和扇形中,一定是轴对称图形的有( )
A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某次体育测试中,九年级一班女同学的一分钟仰卧起坐成绩(单位:个)如下表:
成绩
45
46
47
48
49
50
人数
1
2
4
2
5
1
这此测试成绩的中位数和众数分别为( )
A.47,49
B.47.5,49
C.48,49
D.48,50 -
科目: 来源: 题型:
查看答案和解析>>【题目】2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31
B.31,32
C.31,31
D.32,35 -
科目: 来源: 题型:
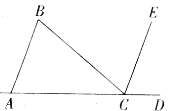
查看答案和解析>>【题目】如图,给出三个论断:①∠A=∠B;② AB//CD;③∠BCD=∠DCE,试回答下列问题:
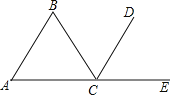
(1)请用其中的两个论断作为条件,另一个作为结论,写出所有的真命题(用序号写出命题,如:如果*、*,那么*);
(2)选择(1)中你写出的任一命题,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两条或两条以上对称轴的轴对称图形是( )
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 锐角三角形
相关试题

