【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
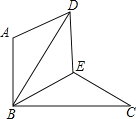
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
参考答案:
【答案】(1)证明见解析(2)菱形,理由见解析
【解析】
试题分析:(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵ ,
,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画图并填空:
如图,△ABC的顶点都在方格纸的格点上,将△ABC向下平移2倍,再向右平移3格.
(1)请在图中画出平移后的△A′B′C′;
(2)在图中画出△的A′B′C′的高C′D′(标出点D′的位置);
(3)如果每个小正方形边长为1,则△A′B′C′的面积= .(答案直接填在题中横线上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
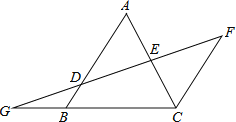
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2﹣4x+c=0不存在实数根,则c的取值范围是( )
A.c>4
B.c≥4
C.c≤4
D.c<4 -
科目: 来源: 题型:
查看答案和解析>>【题目】最大的负整数是_____.
相关试题

