【题目】计算或化简:
(1)(﹣1)2015﹣2﹣1+(π﹣3.14)0
(2)a3﹒a3+(﹣2a3)2﹣a8÷a2
(3)﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
(4)(x+3y﹣4z)(x﹣3y+4z)
参考答案:
【答案】
(1)解:(﹣1)2015﹣2﹣1+( π﹣3.14)0
=﹣1﹣ ![]() +1
+1
=﹣ ![]()
(2)解:a3﹒a3+(﹣2 a3)2﹣a8÷a2
=a6+4a6﹣a6
=4a6
(3)解:﹣5x(﹣x2+2x+1)﹣(2x﹣3)(5+x2)
=5x3﹣10 x2﹣5x﹣(10 x+2x3﹣15﹣3 x2)
=3 x3﹣7 x2﹣15x+15
(4)解:(x+3y﹣4z)(x﹣3y+4z)
=[x+(3y﹣4z)][x﹣(3y﹣4z)]
=x2﹣(3y﹣4z)2
=x2﹣9 y2+24 yz﹣16z2
【解析】(1)根据零指数幂和负整数指数幂计算即可;(2)根据整式的混合计算解答即可;(3)根据整式的混合计算解答即可;(4)根据整式的混合计算解答即可.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).
-
科目: 来源: 题型:
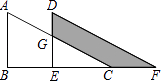
查看答案和解析>>【题目】如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF= .
-
科目: 来源: 题型:
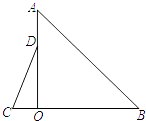
查看答案和解析>>【题目】如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△AOB绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示的正三角形纸板的边长为1,周长记为P1,沿图①的底边剪去一块边长为
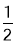 的正三角形纸板后得到图②,然后沿同一底边一次剪去一块更小的正三角板(即其边长为前一块被减掉正三角形纸板边长的
的正三角形纸板后得到图②,然后沿同一底边一次剪去一块更小的正三角板(即其边长为前一块被减掉正三角形纸板边长的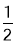 )后,得图③,图④,…,记第n(n≥3)块纸板的周长为Pn,则Pn﹣Pn﹣1= (用含n的代数式表示)
)后,得图③,图④,…,记第n(n≥3)块纸板的周长为Pn,则Pn﹣Pn﹣1= (用含n的代数式表示)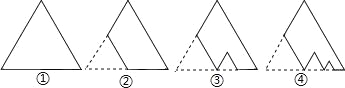
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC,∠ABC=∠ACB。
(1)尺规作图:过顶点A作△ABC的角平分线AD;(不写作法,保留作图痕迹)
(2)在AD上任取一点E(不与点A、D重合),连结BE,CE,求证:EB=EC。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的边OA=4,OC=3,且顶点A、C均在坐标轴上,动点M从点A出发,以每秒1个单位长度的速度沿AO向终点O移动;点N从点C出发沿CB向终点B以同样的速度移动,当两个动点运动了x秒(0<x<4)时,过点N作NP⊥BC交BO于点P,连接MP.
(1)直接写出点B的坐标,并求出点P的坐标(用含x的式子表示);
(2)设△OMP的面积为S,求S与x之间的函数表达式;若存在最大值,求出S的最大值;
(3)在两个动点运动的过程中,是否存在某一时刻,使△OMP是等腰三角形?若存在,求出x的值;若不存在,请说明理由.
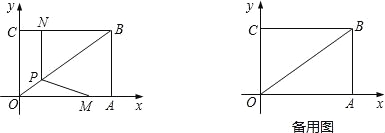
-
科目: 来源: 题型:
查看答案和解析>>【题目】a+b=5,ab=2,则(a﹣2)(3b﹣6)= .
相关试题

