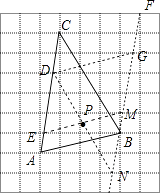
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) ![]() .
.
参考答案:
【答案】
(1)![]()
(2)
如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求
【解析】解:(1)AB= ![]() =
= ![]() .
.
所以答案是 ![]() .(2)如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求.
.(2)如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求.
理由:平行四边形ABME的面积:平行四边形CDNB:平行四边形DEMG=1:2:3,
△PAB的面积= ![]() 平行四边形ABME的面积,△PBC的面积=
平行四边形ABME的面积,△PBC的面积= ![]() 平行四边形CDNB的面积,△PAC的面积=△PNG的面积=
平行四边形CDNB的面积,△PAC的面积=△PNG的面积= ![]() △DGN的面积=
△DGN的面积= ![]() 平行四边形DEMG的面积,
平行四边形DEMG的面积,
∴S△PAB:S△PBC:S△PCA=1:2:3.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣
 x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 AM+CM它的最小值.
AM+CM它的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )
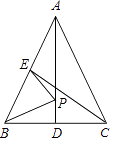
A.BC
B.CE
C.AD
D.AC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
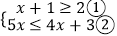 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(1)解不等式①,得;
(2)解不等式②,得;
(3)把不等式①和②的解集在数轴上表示出来: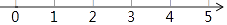
(4)原不等式组的解集为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(1)本次接受调查的跳水运动员人数为 , 图①中m的值为;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;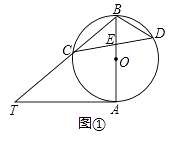
(2)如图②,当BE=BC时,求∠CDO的大小.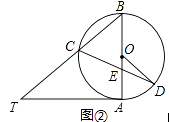
相关试题

