【题目】如图,抛物线y=﹣x2+bx+c与直线AB交于A(﹣4,﹣4),B(0,4)两点,直线AC:y=﹣ ![]() x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
x﹣6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
(1)求抛物线y=﹣x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A,E,F,H为顶点的四边形是矩形?求出此时点E,H的坐标;
②在①的前提下,以点E为圆心,EH长为半径作圆,点M为⊙E上一动点,求 ![]() AM+CM它的最小值.
AM+CM它的最小值.
参考答案:
【答案】
(1)
解:∵点A(﹣4,﹣4),B(0,4)在抛物线y=﹣x2+bx+c上,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+4;
(2)
解:设直线AB的解析式为y=kx+n过点A,B,
∴ ![]() ,
,
∴ ![]() ,
,
∴直线AB的解析式为y=2x+4,
设E(m,2m+4),
∴G(m,﹣m2﹣2m+4),
∵四边形GEOB是平行四边形,
∴EG=OB=4,
∴﹣m2﹣2m+4﹣2m﹣4=4,
∴m=﹣2,
∴G(﹣2,4);
(3)
解:①如图1,
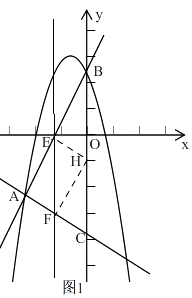
由(2)知,直线AB的解析式为y=2x+4,
∴设E(a,2a+4),
∵直线AC:y=﹣ ![]() x﹣6,
x﹣6,
∴F(a,﹣ ![]() a﹣6),
a﹣6),
设H(0,p),
∵以点A,E,F,H为顶点的四边形是矩形,
∵直线AB的解析式为y=2x+4,直线AC:y=﹣ ![]() x﹣6,
x﹣6,
∴AB⊥AC,
∴EF为对角线,
∴ ![]() (﹣4+0)=
(﹣4+0)= ![]() (a+a),
(a+a), ![]() (﹣4+p)=
(﹣4+p)= ![]() (2a+4﹣
(2a+4﹣ ![]() a﹣6),
a﹣6),
∴a=﹣2,P=﹣1,
∴E(﹣2,0).H(0,﹣1);
②如图2,
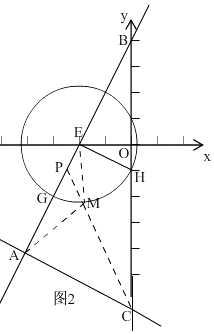
由①知,E(﹣2,0),H(0,﹣1),A(﹣4,﹣4),
∴EH= ![]() ,AE=2
,AE=2 ![]() ,
,
设AE交⊙E于G,取EG的中点P,
∴PE= ![]() ,
,
连接PC交⊙E于M,连接EM,
∴EM=EH= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠PEM=∠MEA,
,∵∠PEM=∠MEA,
∴△PEM∽△MEA,
∴ ![]() ,
,
∴PM= ![]() AM,
AM,
∴ ![]() AM+CM的最小值=PC,
AM+CM的最小值=PC,
设点P(p,2p+4),
∵E(﹣2,0),
∴PE2=(p+2)2+(2p+4)2=5(p+2)2,
∵PE= ![]() ,
,
∴5(p+2)2= ![]() ,
,
∴p=﹣ ![]() 或p=﹣
或p=﹣ ![]() (由于E(﹣2,0),所以舍去),
(由于E(﹣2,0),所以舍去),
∴P(﹣ ![]() ,﹣1),
,﹣1),
∵C(0,﹣6),
∴PC= ![]() =
= ![]() ,
,
即: ![]() AM+CM=
AM+CM= ![]() .
.
【解析】(1)利用待定系数法求出抛物线解析式;(2)先利用待定系数法求出直线AB的解析式,进而利用平行四边形的对边相等建立方程求解即可;(3)①先判断出要以点A,E,F,H为顶点的四边形是矩形,只有EF为对角线,利用中点坐标公式建立方程即可;②先取EG的中点P进而判断出△PEM∽△MEA即可得出PM= ![]() AM,连接CP交圆E于M,再求出点P的坐标即可得出结论.
AM,连接CP交圆E于M,再求出点P的坐标即可得出结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+3交y轴于点A,交反比例函数y=
 (k<0)的图象于点D,y=
(k<0)的图象于点D,y=  (k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD.
(k<0)的图象过矩形OABC的顶点B,矩形OABC的面积为4,连接OD. 
(1)求反比例函数y= 的表达式;
的表达式;
(2)求△AOD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】“兰州中山桥“位于兰州滨河路中段白塔山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥“之美誉.它像一部史诗,记载着兰州古往今来历史的变迁.桥上飞架了5座等高的弧形钢架拱桥. 小芸和小刚分别在桥面上的A,B两处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
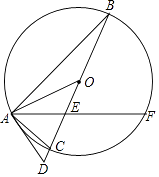
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )
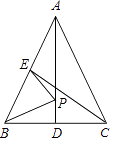
A.BC
B.CE
C.AD
D.AC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD和正方形EFCG的边长分别为3和1,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.

(1)AB的长等于;
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明) .
.
相关试题

