【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
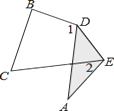
A. ∠A=∠1-∠2 B. 2∠A=∠1-∠2 C. 3∠A=2∠1-∠2 D. 3∠A=2(∠1-∠2)
参考答案:
【答案】B
【解析】
本题求的是∠A、∠1、∠2之间的数量关系,首先画出折叠前的三角形,设为△BCF,可根据三角形的外角性质,首先表示出∠DEF的度数,进而根据三角形内角和定理,得到所求的结论.
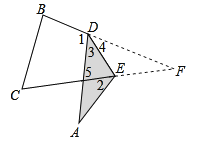
如图,设翻折前A点的对应点为F.根据折叠的性质知:∠3=∠4,∠F=∠A.
由三角形的外角性质知:∠DEF=∠5+∠3=∠A+∠2+∠3.
在△DEF中,∠DEF=180°﹣∠4﹣∠F,故180°﹣∠4﹣∠F=∠A+∠2+∠3,即:
180°﹣∠4﹣∠A=∠A+∠2+∠3,180°﹣∠4﹣∠3=2∠A+∠2,即∠1=2∠A+∠2,2∠A=∠1﹣∠2.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=
 ∠BOC说明理由.
∠BOC说明理由.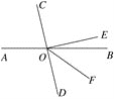
理由:因为∠AOC=∠BOD( ),
∠BOF=
 ∠BOD( ),
∠BOD( ),所以∠BOF=
 ∠AOC( ).
∠AOC( ).因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-
 ∠BOC.
∠BOC.因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°
 ∠BOC)( )
∠BOC)( )所以∠EOF=
 ∠BOC.
∠BOC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.
(1)试指出BC、DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.

-
科目: 来源: 题型:
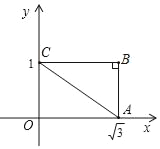
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠ACB=30°,其直角边分别与坐标轴垂直,已知顶点的坐标为A(
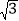 ,0),C(0,1).
,0),C(0,1).(1)如果A关于BC对称的点是D,则点D的坐标为 ;
(2)过点B作直线m∥AC,交CD连线于E,求△BCE的面积.
-
科目: 来源: 题型:
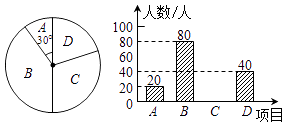
查看答案和解析>>【题目】某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,其中A所在扇形的圆心角为30°,则在被调查的学生中选择跳绳的人数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转90°,点B、D分别落在点B′,D′处,且点A,B′,D′在同一直线上,则tan∠DAD′ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC=4.点P是△ABC内的一点,连接PC,以PC为直角边在PC的右上方作等腰直角三角形PCD.连接AD,若AD∥BC,且四边形ABCD的面积为12,则BP的长为 .

相关试题

