Question

【题目】我们知道，如果两个三角形全等，则它们面积相等，而两个不全等的三角形，在某些情况下，可通过证明等底等高来说明它们的面积相等．已知△ABC与△DEC是等腰直角三角形，∠ACB=∠DCE=90°，连接AD、BE．

（1）如图1，当∠BCE=90°时，求证：S△ACD=S△BCE；
（2）如图2，当0°＜∠BCE＜90°时，上述结论是否仍然成立？如果成立，请证明；如果不成立，说明理由．
（3）如图3，在（2）的基础上，作CF⊥BE，延长FC交AD于点G，求证：点G为AD中点．

Answer 1

【答案】
（1）证明：∵△ABC与△DEC是等腰直角三角形，

∴AC=BC，DC=EC，∠ACB=∠DCE

∵∠BCE=90°，

∴∠ACE=∠BCE，

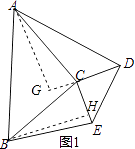
在△ACD与△BCE中，

，

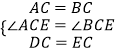∴△ACD≌△BCE（SAS），

∴S△ACE=S△BCE

（2）证明：作AG垂直DC的延长线于点G，作BH⊥CE，垂足为H，

∵∠ACB=∠GCE=90°，

∴∠ACG=∠BCH，

在△ACG与△BCF中，

，

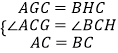∴△ACG≌△BCH（AAS）

∴AG=BH

∵CD=CE

∴ CDAG= CEBH，

即S△ACE=S△BCE

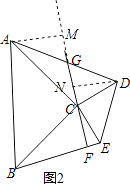
（3）证明：作AM垂直CG的延长线于点M，作DN⊥CG，垂足为N，

∴∠ACB=90，∠BFC=90°，

∴∠ACM+∠BCF=90°，∠BCF+∠CBF=90°，

∴∠ACM=∠CBF，

在△ACM与△BCF中，

，

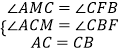∴△ACM≌△CBF（AAS），

∴AM=CF，

同理可证△DCN≌△CEF，

∴DN=CF，

∴AM=DN，

又∵∠AMG=∠DNG，

∴∠AGM=∠DGN，

在△AMG与△DNG中，

，

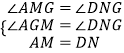∴△AMG≌△DNG（AAS），

∴AG=DG，

即G为AD中点，

【解析】（1）根据△ABC与△DEC是等腰直角三角形，得到AC=BC，DC=EC，∠ACB=∠DCE由∠BCE=90°，证得∠ACE=∠BCE，推出△ACD≌△BCE，从而证得结论S△ACE=S△BCE；（2）作AG垂直DC的延长线于点G，作BH⊥CE，垂足为H，由于∠ACB=∠GCE=90°，得到∠ACG=∠BCH，推出△ACG≌△BCH，得出AG=BH，由于CD=CE，于是得到结果即S△ACE=S△BCE；（3）作AM垂直CG的延长线于点M，作DN⊥CG，垂足为N，证得△ACM≌△CBF，得到AM=CF，同理可证△DCN≌△CEF，得到DN=CF，AM=DN，推出△AMG≌△DNG，得到AG=DG，即G为AD中点．
【考点精析】本题主要考查了等腰直角三角形的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°才能正确解答此题．