【题目】如图,点E,点F分别在菱形ABCD的边AB,AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若 ![]() =2,则
=2,则 ![]() 的值为( )
的值为( )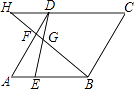
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵AF=2DF,设DF=a,则DF=AE=a,AF=EB=2a,
∵HD∥AB,
∴△HFD∽△BFA,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴HD=1.5a, ![]() =
= ![]() ,
,
∴FH= ![]() BH,
BH,
∵HD∥EB,
∴△DGH∽△EGB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BG= ![]() HB,
HB,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】根据题目的已知条件,利用菱形的性质和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,AC=BC=4,以BC为直径作半圆,圆心为O.以点C为圆心,BC为半径作弧AB,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则
 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,解决提出的问题:
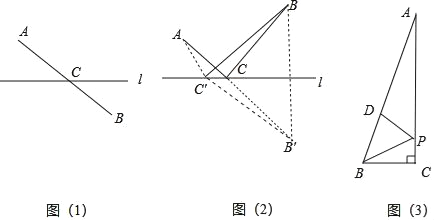
最短路径问题:如图(1),点A,B分别是直线l异侧的两个点,如何在直线l上找到一个点C,使得点C到点A,点B的距离和最短?我们只需连接AB,与直线l相交于一点,可知这个交点即为所求.
如图(2),如果点A,B分别是直线l同侧的两个点,如何在l上找到一个点C,使得这个点到点A、点B的距离和最短?我们可以利用轴对称的性质,作出点B关于的对称点B,这时对于直线l上的任一点C,都保持CB=CB,从而把问题(2)变为问题(1).因此,线段AB与直线l的交点C的位置即为所求.
为了说明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′.因为AB′≤AC′+C′B′,∴AC+CB<AC'+C′B,即AC+BC最小.
任务:
数学思考
(1)材料中划线部分的依据是 .
(2)材料中解决图(2)所示问题体现的数学思想是 .(填字母代号即可)
A.转化思想
B.分类讨论思想
C.整体思想
迁移应用
(3)如图,在Rt△ABC中,∠C=90°,∠BAC=15°,点P为C边上的动点,点D为AB边上的动点,若AB=8cm,则BP+DP的最小值为 cm.
-
科目: 来源: 题型:
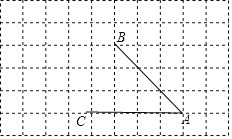
查看答案和解析>>【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线 的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技与经济的发展,机器人自动化线的市场越来越大,并且逐渐成为自动化生产线的主要方式某化工厂要在规定时间内搬运1800千克化工原料,现有A,B两种机器人可供选择,已知A型机器人每小时完成的工作量是B型机器人的1.5倍,A型机器人单独完成所需的时间比B型机器人少10小时.
(1)求两种机器人每小时分别搬运多少千克化工原料?
(2)若A型机器人工作1小时所需的费用为80元,B型机器人工作1小时所需的费用为60元,若该工厂在两种机器人中选择其中的一种机器人单独完成搬运任务,则选择哪种机器人所需费用较小?请计算说明.
相关试题

