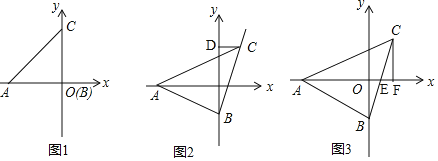
【题目】已知,△ABC满足BC=AB,∠ABC=90°,A点在x轴的负半轴上,直角顶点B在y轴上,点C在x轴上方.
(1)如图1所示,若A的坐标是(-3,0),点B与原点重合,则点C的坐标是_________;
(2)如图2,过点C作CD⊥y轴于D,请判断线段OA、OD、CD之间的数量关系并说明理由;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于点F,问CF与AE有怎样的数量关系?并说明理由.
参考答案:
【答案】(1)C(0,3);(2)OA=OD+CD;(3)AE=2CF.
【解析】试题分析:(1)根据点![]() 可得点
可得点![]() 坐标;
坐标;
![]() 证明
证明![]() 得到
得到![]() 即可解答;
即可解答; ![]() 如图3,延长
如图3,延长![]() 相交于
相交于![]() ,证明
,证明![]() 得到
得到![]() ,再证明
,再证明![]() 得到
得到![]() 即可解答.
即可解答.
试题解析:(1)∵BC=AB,且A的坐标是(3,0),
∴BC=BA=3,
∴点C的坐标为(0,3),
故答案为:(0,3);
(2)OA=OD+CD;
∵CD⊥y轴,
![]()
![]()
![]()
∴∠ABO=∠DCB,
在△ABO和△BCD中,

![]()
∴BO=CD,OA=DB,
∵BD=OB+OD,
∴OA=CD+OD.
(3)AE=2CF,
如图3,延长CF,AB相交于G,

∵x轴恰好平分∠BAC,
∴∠CAF=∠GAF,
∵CF⊥x轴,
∴∠AFE=∠AFG=90,
在△AFC和△AFG中,
∵
![]()
∴CF=GF,
![]()
∴∠BAE=∠BCG,
在△ABE和△CBG中,
∵
![]()
∴AE=CG,
∴AE=CF+GF=2CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,2)关于y轴对称的点的坐标为( )
A. (3,﹣2) B. (3,2) C. (﹣3,﹣2) D. (2,﹣3)
-
科目: 来源: 题型:
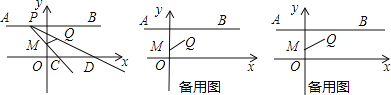
查看答案和解析>>【题目】已知如图,在平面直角坐标系中有四点,坐标分别为A(-4,3)、B(4,3)、M(0,1)、Q(1,2),动点P在线段AB上,从点A出发向点B以每秒1个单位运动.连接PM、PQ并延长分别交x轴于C、D两点(如图).
(1)在点P移动的过程中,若点M、C、D、Q能围成四边形,则t的取值范围是_________,并写出当t=2时,点C的坐标______________.
(2)在点P移动的过程中,△PMQ可能是轴对称图形吗?若能,请求出符合条件的点P的坐标;若不能,请说明理由.
(3)在点P移动的过程中,求四边形MCDQ的面积S的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上全班男生进行了百米测试,达标成绩为14秒,下面是第一小组8名男生的成绩记录,其中“+”表示成绩大于14秒,“﹣”表示成绩小于14秒
﹣1
+0.8
0
﹣1.2
﹣0.1
0
+0.5
﹣0.6
(1)求这个小组的男生达标率是多少?
(2)求这个小组8名男生的平均成绩是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴.如果A点坐标是(1,2
 ),C点坐标是(3,-2
),C点坐标是(3,-2 ).
).(1)求B点和D点的坐标;
(2)将这个长方形向下平移
 个单位长度,四个顶点的坐标变为多少?请你写出平移后四个顶点的坐标;
个单位长度,四个顶点的坐标变为多少?请你写出平移后四个顶点的坐标;(3)如果Q点以每秒
 米的速度在长方形ABCD的边上从A出发到C点停止,沿着A→D→C的路径运动,那么当Q点的运动时间分别是1秒、4秒和6秒时,△BCQ的面积各是多少?请你分别求出来.
米的速度在长方形ABCD的边上从A出发到C点停止,沿着A→D→C的路径运动,那么当Q点的运动时间分别是1秒、4秒和6秒时,△BCQ的面积各是多少?请你分别求出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 2018年10月24日港珠澳大桥正式通车港珠澳大桥是在“一国两制”方针下,粤港澳三地首次合作共建的超大型基础设施项目,大桥全长55000米.将数据55000用科学记数法可表示为( )
A. 5.5×103B. 5.5×104C. 55×103D. 0.55×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对数中,数值相等的是( )
A.23和32
B.(﹣2)2和﹣22
C.2和|﹣2|
D.( )2和
)2和 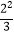
相关试题

