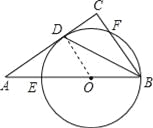
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD.欲证AC是⊙O的切线,只需证明AC⊥OD即可;
(2)利用平行线截线段成比例推知![]() ;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
;然后将图中线段间的和差关系代入该比例式,通过解方程即可求得r的值,即⊙O的半径r的值.
试题解析:(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB(等角对等边);
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ODB=∠DBC(等量代换),
∴OD∥BC(内错角相等,两直线平行);
又∵∠C=90°(已知),
∴∠ADO=90°(两直线平行,同位角相等),
∴AC⊥OD,即AC是⊙O的切线;
(2)解:由(1)知,OD∥BC,
∴![]() (平行线截线段成比例),
(平行线截线段成比例),
∴![]() ,
,
解得r=![]() ,即⊙O的半径r为
,即⊙O的半径r为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列命题中,为真命题的是( )
A. 相等的角是对顶角 B. 平行于同一条直线的两条直线互相平行
C. 同旁内角互补 D. 垂直于同一条直线的两条直线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
A.沙漠
B.体温
C.时间
D.骆驼 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确有( )个。
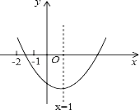
A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】大学生小刘回乡创办小微企业,初期购得原材料若干吨,每天生产相同件数的某种产品,单件产品所耗费的原材料相同.当生产6天后剩余原材料36吨,当生产10天后剩余原材料30吨.若剩余原材料数量小于或等于3吨,则需补充原材料以保证正常生产.
(1)求初期购得的原材料吨数与每天所耗费的原材料吨数;
(2)若生产16天后,根据市场需求每天产量提高20%,则最多再生产多少天后必须补充原材料?
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图 (如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c ),大正方形的面积可以表示为c2,也可以表示为4×
 ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,那么a2+b2=c2.
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,那么a2+b2=c2.

(1) 图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2) 如图③,在Rt△ABC中,∠ACB=90°,AC=3 cm,BC=4 cm,则斜边AB上的高CD的长为________cm.
(3) 试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在图④的网格中,并标出字母a,b所表示的线段.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
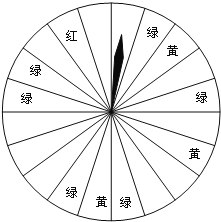
(1)求他此时获得购物券的概率是多少?
(2)他获得哪种购物券的概率最大?请说明理由.
相关试题

