【题目】已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.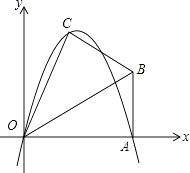
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:过点C作CH⊥x轴,垂足为H;
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,
∴OB=4,OA=2 ![]() ;
;
由折叠的性质知:∠COB=30°,OC=AO=2 ![]() ,
,
∴∠COH=60°,OH= ![]() ,CH=3;
,CH=3;
∴C点坐标为( ![]() ,3)
,3)
(2)解:∵抛物线y=ax2+bx(a≠0)经过C( ![]() ,3)、A(2
,3)、A(2 ![]() ,0)两点,
,0)两点,
∴ ![]() ,
,
解得 ![]() ;
;
∴此抛物线的函数关系式为:y=﹣x2+2 ![]() x
x
(3)解:存在.
∵y=﹣x2+2 ![]() x的顶点坐标为(
x的顶点坐标为( ![]() ,3),
,3),
即为点C,MP⊥x轴,垂足为N,设PN=t;
∵∠BOA=30°,
∴ON= ![]() t,
t,
∴P( ![]() t,t);
t,t);
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E;
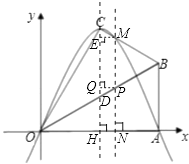
把x= ![]() t代入y=﹣x2+2
t代入y=﹣x2+2 ![]() x,
x,
得y=﹣3t2+6t,
∴M( ![]() t,﹣3t2+6t),E(
t,﹣3t2+6t),E( ![]() ,﹣3t2+6t),
,﹣3t2+6t),
同理:Q( ![]() ,t),D(
,t),D( ![]() ,1);
,1);
要使四边形CDPM为等腰梯形,只需CE=QD,
即3﹣(﹣3t2+6t)=t﹣1,
解得t= ![]() ,t=1(舍去),
,t=1(舍去),
∴P点坐标为( ![]() ,
, ![]() ),
),
∴存在满足条件的P点,使得四边形CDPM为等腰梯形,此时P点坐标为( ![]() ,
, ![]() )
)
【解析】(1)根据直角三角形的性质,求出OA、OB的值,由折叠的性质,得到C点坐标;(2)由抛物线经过C、A两点,由待定系数法求出抛物线的函数关系式;(3)根据抛物线的解析式,求出抛物线的顶点坐标,由∠BOA=30°,得到P点的坐标,求出M、E、Q、D的坐标,根据要使四边形CDPM为等腰梯形,只需CE=QD,求出P点坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合).
(1)如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;
(2)如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).

-
科目: 来源: 题型:
查看答案和解析>>【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米)
运费(元/吨千米)
甲库
乙库
甲库
乙库
A库
20
15
12
12
B库
25
20
10
8
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在ΔABC外的点
 处,若∠1=20°,则∠2的度数为( )
处,若∠1=20°,则∠2的度数为( ) 
A. 80°B. 90°
C. 100°D. 110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】【发现证明】如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
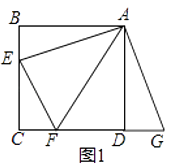
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;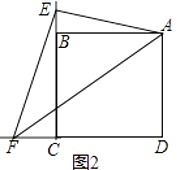
(2)【联想拓展】如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.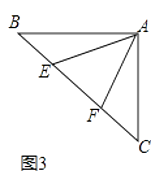
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数
 于点(2,a),求:
于点(2,a),求:(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
相关试题

