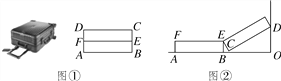
【题目】如图①所示的旅行箱的箱盖和箱底两部分的厚度相同,四边形ABCD为形如矩形的旅行箱一侧的示意图,F为AD的中点,EF∥CD.现将放置在地面上的箱子打开,使箱盖的一端点D靠在墙上,O为墙角,图②为箱子打开后的示意图.箱子厚度AD=30cm,宽度AB=50cm.
(1)图②中,EC=________cm,当点D与点O重合时,AO的长为________cm;
(2)若∠CDO=60°,求AO的长(结果取整数值,参考数据:sin60°≈0.87,cos60°=0.5,tan60°≈1.73,可使用科学计算器).
参考答案:
【答案】(1)15,100(2)101cm
【解析】试题分析: (1)根据EC=![]() BC=
BC=![]() AD,AO=AB+CD=2AB即可解决问题.
AD,AO=AB+CD=2AB即可解决问题.
(2)过点C作OA的平行线,分别交BE和OD于H,G,根据∠CDO=60°,分别求出CG、HC,即可解决问题.
试题解析:
(1)根据图①,EF∥AB∥CD,F为AD的中点,∴DF=AF,∴EC=EB=![]() BC=
BC=![]() AD=15cm.根据图②,当点D与点O重合时,BO=CD.∵CD=AB=50cm,∴AO=AB+BO=AB+CD=50+50=100(cm).
AD=15cm.根据图②,当点D与点O重合时,BO=CD.∵CD=AB=50cm,∴AO=AB+BO=AB+CD=50+50=100(cm).
故答案为15,100.
(2)过点C作OA的平行线,分别交BE和OD于H,G.
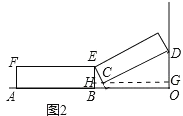
∵EB⊥OA,OD⊥OA,
又∵∠O=90°,
∴四边形BOGH是矩形.
∴BO=HG=HC+CG.
∵∠CGD=∠ECD=90°,∠CDO=60°,
∴∠DCG=90°-∠CDG=30°,
∴∠ECH=180°-∠ECD-∠DCG=180°-90°-30°=60°.
在Rt△CDG和Rt△ECH中,CD=50cm,EC=15cm,
∴HC=EC·cos∠ECH=7.5cm,
CG=CD·sin∠CDG≈50×0.87=43.5(cm),
∴AO=AB+BO=AB+HC+CG≈101cm.
点睛: 本题考查解直角三角形的应用,解题的关键是理解题意,学会添加常用辅助线解决问题,通过添加辅助线构造直角三角形以及特殊四边形,属于中考常考题型.
-
科目: 来源: 题型:
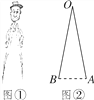
查看答案和解析>>【题目】如图①是一副创意卡通圆规,图②是其平面示意图,OA是支撑臂,OB是旋转臂.使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18°时,求所作圆的半径(结果精确到0.01cm);
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度(结果精确到0.01cm,参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器).
-
科目: 来源: 题型:
查看答案和解析>>【题目】南京规划地铁6号线由栖霞山站开往南京南站,全长32100米,这个数据用科学记数法表示为( )
A.321×102
B.32.1×103
C.3.21×104
D.3.21×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2+3x+1=0的根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.没有实数根
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+
 m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )A. 0 B. 1 C. 2 D. 与m有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个角的补角比这个角的余角的3倍大10°,则这个角的度数是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市老板到批发中心选购甲、乙两种品牌的文具盒共
 个,乙品牌的进货单价比甲品牌进货单价多
个,乙品牌的进货单价比甲品牌进货单价多 元,当购进甲品牌的文具盒
元,当购进甲品牌的文具盒 个时,购进甲、乙品牌文具盒共需
个时,购进甲、乙品牌文具盒共需 元.
元.(
 )求甲、乙两种品牌的的文具盒进货单价.
)求甲、乙两种品牌的的文具盒进货单价.(
 )若该超市每销售
)若该超市每销售 个甲种品牌的文具盒可获利
个甲种品牌的文具盒可获利 元,每销售
元,每销售 个乙种品牌的文具盒可获利
个乙种品牌的文具盒可获利 元,根据学生需求,超市老板决定,准备用不超过
元,根据学生需求,超市老板决定,准备用不超过 元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获得不低于
元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获得不低于 元,问该超市有几种进货方案,分别是什么方案.
元,问该超市有几种进货方案,分别是什么方案.(
 )哪种方案能使获利最大,最大获得为多少元.
)哪种方案能使获利最大,最大获得为多少元.
相关试题

