【题目】正方形网格中(网格中的每个小正方形边长是1),![]() 的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1) 作出![]() 绕点A逆时针旋转90°的
绕点A逆时针旋转90°的![]() ,再作出
,再作出![]() 关于原点O成中心对称的
关于原点O成中心对称的![]() .
.
(2)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 .
的坐标为 .
(3)![]() 经过怎样的旋转可得到
经过怎样的旋转可得到![]() , .
, .
参考答案:
【答案】(1)作图见解析;(2)(-2,-3),(3,1);(3)△ABC绕点(0,-1)顺时针旋转90°.
【解析】
试题分析:(1)根据网格结构找出点B、C的对应点B1、C1的位置,然后顺次连接即可,再找出点A1、B2、C2的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标;
(3)根据图形,利用旋转的旋转解答.
试题解析:(1)△AB1C1,△A1B2C2如图所示;
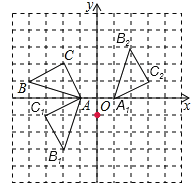
(2)B1(-2,-3),C2(3,1);
(3)△ABC绕点(0,-1)顺时针旋转90°得到△A1B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若向东走5m,记为+5m,则﹣3m表示为( )
A.向东走3m
B.向南走3m
C.向西走3m
D.向北走3m -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题是真命题的是( )
A. 如果a>0,b>0,则a+b>0
B. 直角都相等
C. 两直线平行,同位角相等
D. 若a=6,则|a|=|6|
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为三角形ABD中线,
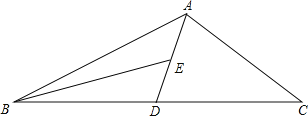
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,一个无盖的长方体盒子的棱长分别为
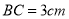 ,
,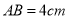 ,
,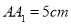 ,盒子的内部顶点
,盒子的内部顶点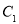 处有一只昆虫甲,在盒子的内部顶点
处有一只昆虫甲,在盒子的内部顶点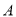 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点
处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点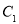 处静止不动,请计算
处静止不动,请计算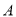 处的昆虫乙沿盒子内壁爬行到昆虫甲
处的昆虫乙沿盒子内壁爬行到昆虫甲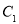 处的最短路程,并画出其最短路径,简要说明画法
处的最短路程,并画出其最短路径,简要说明画法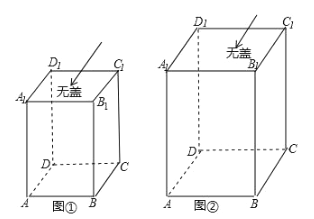
(2)如果(1)问中的长方体的棱长分别为
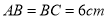 ,
,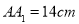 ,如图②,假
,如图②,假设昆虫甲从盒内顶点
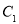 以1厘米/秒的速度在盒子的内部沿棱
以1厘米/秒的速度在盒子的内部沿棱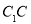 向下爬行,同时昆虫乙从
向下爬行,同时昆虫乙从盒内顶点
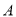 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕
以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
-
科目: 来源: 题型:
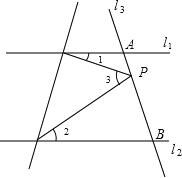
查看答案和解析>>【题目】如图,已知直线l1// l2, 且l3和l1, l2分别交于A,B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在点A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化;(不说明理由)
(3)如果点P在点A、B两点外侧运动时,直接写出∠1、∠2、∠3之间的关系;(点P和点A、B不重合)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市6月份某周内每天的最高气温数据如下(单位:℃):24 26 29 26 29 32 29
则这组数据的众数和中位数分别是( )
(A)29,29.(B)26,26.(C)26,29. (D)29,32.
相关试题

