【题目】我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.
如图1,在四边形![]() 中,
中,![]() ,四边形
,四边形![]() 就是“正交四边形”.
就是“正交四边形”.
(1)下列四边形,一定是“正交四边形”的是______.
①平行四边形②矩形③菱形④正方形
(2)如图2,在“正交四边形”![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
(3)小明说:“计算‘正交四边形’的面积可以仿照菱形的方法,面积是对角线之积的一半.”小明的说法正确吗?如果正确,请给出证明;如果错误,请给出反例.
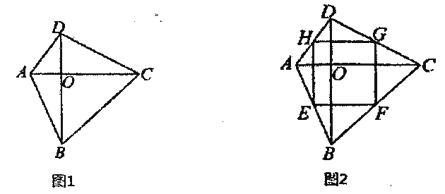
参考答案:
【答案】(1)③④ ;(2)详见解析;(3)小明的说法正确.
【解析】
(1)由特殊四边形的性质,可知菱形和正方形的对角线互相垂直;
(2)首先根据三角形中位线定理和平行四边形的判定定理证明四边形EFGH是平行四边形,然后再证明HG⊥HE即可;
(3)由![]() ,根据三角形的面积公式进行求解即可.
,根据三角形的面积公式进行求解即可.
答:(1)③④
(2)证明:∵![]() 分别是
分别是![]() 的中点∴
的中点∴![]() ,
,![]()
∵![]() 分别是
分别是![]() 的中点∴
的中点∴![]() ,
,![]()
∴![]() ,
,![]() .∴四边形
.∴四边形![]() 是平行四边形
是平行四边形
∵![]() 分别是
分别是![]() 的中点
的中点
∴![]()
∵四边形![]() 是“正交四边形”
是“正交四边形”
∴![]()
∴![]()
∴四边形![]() 是矩形
是矩形
(3)答:小明的说法正确.
证明:![]()
![]()
-
科目: 来源: 题型:
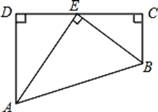
查看答案和解析>>【题目】如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,求CB的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点分别为
 ,
, 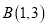 ,
,  .若反比例函数
.若反比例函数 在第一象限内的图象与△ABC有公共点,则k的取值范围是__________.
在第一象限内的图象与△ABC有公共点,则k的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
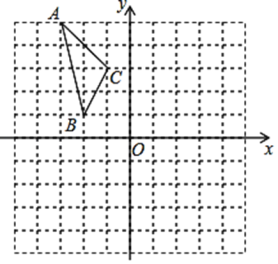
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出图形并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点C按顺时针方向旋转90°得到△A2B2C2,画出图形,求出线段CA扫过的部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1所示,在△ABC中,若AB=AC,∠BAC=120°,AB的垂直平分线交BC于点M,交AB于点E.AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN,试判断△AMN的形状,并证明你的结论.
(2)如图2所示,在△ABC中,若∠C=45°,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,连接AM、AN,若AC=3
 ,BC=8,求MN的长.
,BC=8,求MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
(2)如图,AB是
 的直径,PA与
的直径,PA与 相切于点A,OP与
相切于点A,OP与 相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
相交于点C,连接CB,∠OPA=40°,求∠ABC的度数.
相关试题

