搜索
【题目】将正整数1至2016按一定规律排列如表：
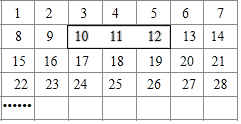
平移表中带阴影的方框，方框中三个数的和可能是（ ）
A.2000B.2019C.2100D.2148
参考答案：
【答案】D
【解析】
相邻三个数按顺序排列可表示为：(x-1)、x、(x+1).
将这三个数加起来分别取等于2000、2019、2100、2148，若x为正数，则满足题意，因此可以求出(x-1)、x、(x+1).
设中间数为x，则另外两个数分别为x﹣1、x+1，
∴三个数之和为（x﹣1）+x+（x+1）＝3x．
根据题意得：3x＝2019、3x＝2000、3x＝2100、3x＝2148，
解得：x＝673，x＝666
（舍去），x＝700，x＝716．
∵673＝96×7+1，
∴2019不合题意，舍去；
∵700＝100×7，
∴2100不合题意，舍去；
∵716＝102×7+2，
∴三个数之和为2148．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：探究一次函数y=kx+k+2（k是不为0常数）图象的共性特点，探究过程：小明尝试把x=-1代入时，发现可以消去k，竟然求出了y=2．老师问：结合一次函数图象，这说明了什么？小组讨论得出：无论k取何值，一次函数y=kx+k+2的图象一定经过定点（-1，2），老师：如果一次函数的图象是经过某一个定点的直线，那么我们把像这样的一次函数的图象定义为“点旋转直线”．已知一次函数y=（k+3）x+（k-1）的图象是“点旋转直线”
（1）一次函数y=（k+3）x+（k-1）的图象经过的定点P的坐标是__________．
（2）已知一次函数y=（k+3）x+（k-1）的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3，求k值；
②若△AOB的面积为1，求k值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表是小明记录的今年雨季一周河水的水位变化情况（上周末的水位达到警戒水位）．
星期
一
二
三
四
五
六
日
水位变化/米
+0.20
+0.81
﹣0.35
+0.03
+0.28
﹣0.36
﹣0.01
注：正号表示水位比前一天上升，负号表示水位比前一天下降．
（1）本周哪一天河流的水位最高？哪一天河流的水位最低？它们位于警戒水位之上还是之下？与警戒水位的距离分别是多少米？
（2）与上周相比，本周末河流水位是上升了还是下降了？
-
科目： 来源： 题型：
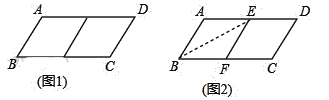
查看答案和解析>>【题目】邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，ABCD中，若AB=1，BC=2，则ABCD为1阶准菱形．
（1）猜想与计算：
邻边长分别为3和5的平行四边形是_______阶准菱形；已知ABCD的邻边长分别为a，b（a＞b），满足a=8b+r，b=5r，请写出ABCD___________阶准菱形．
（2）操作与推理：
小明为了剪去一个菱形，进行了如下操作：如图2，把ABCD沿BE折叠（点E在AD上），使点A落在BC边上的点F处，得到四边形ABFE．请证明四边形ABFE是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=
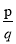，例如12可以分解成1×12,2×6或3×4，因为12-1＞6-2＞4-3，所有3×4是最佳分解，所以F（12）=
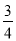.（1）如果一个正整数a是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1.
（2）如果一个两位正整数t，t=10x+y（1≤x≤y≤9,x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y=ax+b的图象过点（﹣2，1），则关于抛物线y=ax2﹣bx+3的三条叙述：其中所有正确叙述的个数是（ ）
①过点（2，1），②对称轴可以是x=1，③当a＜0时，其顶点的纵坐标的最小值为3．
A. 0 B. 1 C. 2 D. 3
相关试题
