【题目】解方程:
(1)(y+1)-2(y-1)=1-3y (2)![]()
(3)![]() (x-3)-
(x-3)-![]() (2x+1)=1 (4)
(2x+1)=1 (4)![]()
参考答案:
【答案】(1)y=-1;(2)x=![]() ;(3)x=-17;(4)x=
;(3)x=-17;(4)x=![]() .
.
【解析】(1)先去括号,再移项、合并、系数化为1即可得解;
(2)先去分母,再去括号,然后移项、合并、系数化为1即可得解.
(3)先去分母,再去括号,然后移项、合并、系数化为1即可得解.
(4)先去分母,再去括号,然后移项、合并、系数化为1即可得解.
解:(1)(y+1)-2(y-1)=1-3y,
去括号得:y+1-2y+2=1-3y,
移项得:y-2y+3y=1-1-2,
合并得:2y=-2,
系数化1得:y=-1;
(2)![]()
去分母得:5(3x+1)-20=3x-2-2(2x+3),
去括号得:15x+5-20=3x-2-4x-6,
移项得:15x-3x+4x=-2-6-5+20,
合并得:16x=7,
系数化1得:x=![]() ;
;
(3)![]() (x-3)-
(x-3)-![]() (2x+1)=1,
(2x+1)=1,
去分母得:3(x-3)-2(2x+1)=6,
去括号得:3x-9-4x-2=6,
移项得:3x-4x=6+2+9,
合并得:-x=17,
系数化1得:x=-17;
(4)![]()
去分母得:2(4x-1)=5x+5,
去括号得:8x-2=5x+5,
移项得:8x-5x=5+2,
合并得:3x=7,
系数化1得:x=![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2、0、1、﹣1这四个数中,最大的有理数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
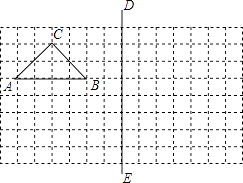
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角互补,那么这两个角可能是
①均为直角;②均为钝角;③一个为锐角,一个为钝角;④以上三者都有可能
A. ①② B. ①③ C. ②③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
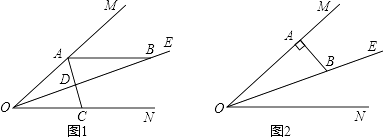
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
相关试题

