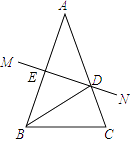
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E. 
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
参考答案:
【答案】
(1)解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°
(2)解:∵MN垂直平分AB,
∴DA=DB,
∵BC+BD+DC=20,
∴AD+DC+BC=20,
∴AC+BC=20,
∵AB=2AE=12,
∴△ABC的周长=AB+AC+BC=12+20=32.
【解析】(1)由在△ABC中,AB=AC,∠A=42°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数.(2)由△CBD的周长为20,推出AC+BC=20,根据AB=2AE=12,由此即可解决问题.
【考点精析】本题主要考查了线段垂直平分线的性质和等腰三角形的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A. 两个全等三角形成轴对称
B. 两个三角形关于某直线对称,不一定全等
C. 线段AB的对称轴垂直平分AB
D. 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过秒时,△DEB与△BCA全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2、0、1、﹣1这四个数中,最大的有理数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)(y+1)-2(y-1)=1-3y (2)
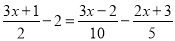
(3)
 (x-3)-
(x-3)- (2x+1)=1 (4)
(2x+1)=1 (4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
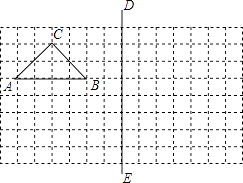
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小.
相关试题

