Question

【题目】如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM＝，ON＝6，点P、Q分别在边OB、OA上，则MP+PQ+QN的最小值是_____．

Answer 1

【答案】

【解析】

作M关于OB的对称点M′，作N关于OA的对称点N′，连接M′N′，即为MP+PQ+QN的最小值；证出△ONN′为等边三角形，△OMM′为等边三角形，得出∠N′OM′＝90°，由勾股定理求出M′N′即可．

解：作M关于OB的对称点M′，作N关于OA的对称点N′，如图所示：

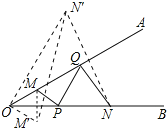
连接M′N′，即为MP+PQ+QN的最小值．

根据轴对称的定义可知：∠N′OQ＝∠M′OB＝30°，∠ONN′＝60°，

∴△ONN′为等边三角形，△OMM′为等边三角形，

∴∠N′OM′＝90°，OM′＝OM＝，ON′＝ON＝6，

∴在Rt△M′ON′中，

M′N′＝＝＝．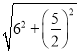

故答案为：．