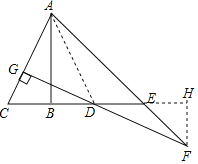
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.

参考答案:
【答案】(1)45°﹣α;(2)相等,理由见解析;(3)EF=3![]() .
.
【解析】
(1)根据等腰三角形的性质得到∠BAE=∠AEB=45°,根据三角形的内角和即可得到结论;
(2)连接AD,根据线段垂直平分线的性质得到AC=AD,求得∠ADC=∠ACB=α,于是得到AC=DF;
(3)根据已知条件得到BD=CB=3,过F作FH⊥CE交CE的延长线于H,得到△EHF是等腰直角三角形,求得FH=HE,根据全等三角形的性质即可得到结论.
解:(1)∵AB⊥CD,
∴∠ABE=90°,
∵AB=BE,
∴∠BAE=∠AEB=45°,
∵∠CAB=α,∠CDG=90°﹣(90°﹣α)=α=∠EDF.
∴∠AFG=∠AED﹣∠EDF=45°﹣α;
故答案为:45°﹣α;
(2)相等,
证明:连接AD,
∵AB垂直平分线段CD,
∴AC=AD,
∴∠ADC=∠ACB=90°﹣α,
∴∠DAE=∠ADC﹣45°=45°﹣α,
∴∠DAE=∠AFD,
∴AD=DF,
∴AC=DF;
(3)∵CD=6,
∴BD=CB=3,
过F作FH⊥CE交CE的延长线于H,
则△EHF是等腰直角三角形,
∴FH=HE,
∵∠H=∠ABC=90°,∠CAB=∠CDG=∠FDH,AC=AD=DF,
∴△ACB≌△DFH(AAS),
∴FH=CB=3,
∴EF=![]() FH=3
FH=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步降低机动车污染物排放,减轻重污染天气污染发生频次和污染程度,保障人民群众身体健康,郑州市从2017年12月4日0时至2017年12月31日24时起对机动车实施单双号限行措施,此次限行将会大大减少空气中
 的排放量,
的排放量, 指的是雾天气时大气中直径小于或等于
指的是雾天气时大气中直径小于或等于 的颗粒物,将
的颗粒物,将 用科学记数法表示为
用科学记数法表示为

A.
 B.
B. 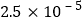 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组)
①

②

把下列各式分解因式:
③
 ;
; ④

化简分式
⑤
 ;
; ⑥(
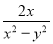 -
- )(x-y)2
)(x-y)2 解方程:
⑦
 ;
; ⑧

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:有一块三角形状的土地平均分给四户人家,现有四种不同的分法,
 如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点
如图中,D、E、F分别是BC、AC、AB的中点,G、H分别是BF、AF的中点 ,其中正确的分法有
,其中正确的分法有


A. 1种 B. 2种 C. 3种 D. 4种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,则AB=_____.

相关试题

