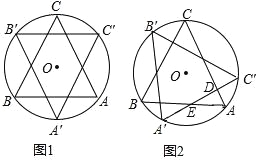
【题目】如图,边长为2的等边△ABC内接于⊙O,△ABC绕圆心O顺时针旋转得到△A′B′C′,A′C′分别交于点E、D,设旋转角为a(0°<a<360°).
(1)当a= 时,△A′′BC′与△ABC出现旋转过程中的第一次完全重合.
(2)当a=60°(如图1),该图
A,是中心对称图形但不是轴对称图形 B.是轴对称图形但不是中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形
(3)如图2,当0°<a<120°时,△ADE的周长是否会发生变化?若会变化,请说明理由,若不会变化,求出它的周长.
参考答案:
【答案】(1)、120°;(2)、C;(3)、2.
【解析】
试题分析:(1)、连接BO与CO,利用圆心角的可得a的度数即可;(2)、根据轴对称图形与中心对称图形的定义判断即可;(3)、连接AA',利用等弦对等弧解答即可.
试题解析:(1)、连接BO与CO,如图1:

∠BOC=![]() ,所以当a=120°时,△A′′BC′与△ABC出现旋转过程中的第一次完全重合,
,所以当a=120°时,△A′′BC′与△ABC出现旋转过程中的第一次完全重合,
(2)、观察图1,可得该图既是轴对称图形又是中心对称图形,故选C,
(3)、△ADE的周长不变,
如图2,连接AA',

∵AB=A'C', ∴![]() ,∴
,∴![]() ,∴∠BAA'=∠AA'C, ∴EA=EA;, 同理DA=DC',
,∴∠BAA'=∠AA'C, ∴EA=EA;, 同理DA=DC',
∴△ADE的周长=EA+ED+DA=EA'+ED+DC'=A'C'=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
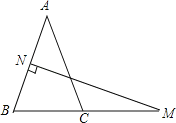
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正十五边形的每一个内角等于___度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,取一张长方形纸片ABCD,沿AD边上任意一点M折叠后,点D、C分别落在D′、C′的位置,设折痕为MN,D′C′交BC于点E且∠AMD′=α,∠NEC′=β
(1)探究α、β之间的数量关系,并说明理由.
(2)连接AD′是否存在折叠后△AD′M与△C′EN全等的情况?若存在,请给出证明;若不存在,请直接作否定的回答,不必说明理由.

-
科目: 来源: 题型:
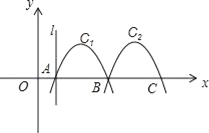
查看答案和解析>>【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个内角是80°,则它的底角是 0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x2+x=x3
B.2x2﹣x2=1
C.x2x=2x2
D.x6÷x3=x3
相关试题

