【题目】如图,取一张长方形纸片ABCD,沿AD边上任意一点M折叠后,点D、C分别落在D′、C′的位置,设折痕为MN,D′C′交BC于点E且∠AMD′=α,∠NEC′=β
(1)探究α、β之间的数量关系,并说明理由.
(2)连接AD′是否存在折叠后△AD′M与△C′EN全等的情况?若存在,请给出证明;若不存在,请直接作否定的回答,不必说明理由.

参考答案:
【答案】(1)、α+β=90°;(2)、点D′与点B重合时,△AD′M与△C′EN全等;证明过程见解析.
【解析】
试题分析:(1)、α+β=90°.如图1,延长MD′交BC于点F.利用平行线的性质得到:∠AM D′=∠MFE=α.然后根据折叠的性质推知:∠MFE+∠D′EF=90°,∠D′EF=∠NEC′,故α+β=90°;(2)、当点D′与点B重合时,△AD′M与△C′EN全等.如图2,此时,B、E、D′三点重合.利用折叠的性质和全等三角形的判定定理HL证得这两个三角形全等;
试题解析:(1)、α+β=90°.理由如下:
如图1,延长MD′交BC于点F.∵AD∥BC, ∴∠AM D′=∠MFE=α.
又∠MD′E=∠D=90°,∠FD′E=90°,∴∠MFE+∠D′EF=90°,∠D′EF=∠NEC′, 故α+β=90°;
(2)、当点D′与点B重合时,△AD′M与△C′EN全等.
如图2,此时,B、E、D′三点重合.∵由折叠可知,∠1=∠2,∴∠C′=∠C=∠A=90°,C′E=CD.
∵AD∥BC,∠2=∠3, 得∠1=∠3,即D′M=EN. 又AD′=DC, ∴AD′=C′E,
∴在Rt△AD′M与Rt△C′EN中,![]() ,故Rt△AD′M≌Rt△C′EN(HL).
,故Rt△AD′M≌Rt△C′EN(HL).


-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店为了解5月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下两幅不完整的统计图

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
类别
篮球
足球
排球
进价(单位:元/个)
50
30
20
预售价(单位:元/个)
70
45
25
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40°.
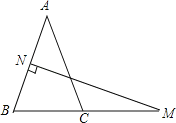
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现∠A与∠NMB有什么关系,试证明之.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正十五边形的每一个内角等于___度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的等边△ABC内接于⊙O,△ABC绕圆心O顺时针旋转得到△A′B′C′,A′C′分别交于点E、D,设旋转角为a(0°<a<360°).
(1)当a= 时,△A′′BC′与△ABC出现旋转过程中的第一次完全重合.
(2)当a=60°(如图1),该图
A,是中心对称图形但不是轴对称图形 B.是轴对称图形但不是中心对称图形
C.既是轴对称图形又是中心对称图形 D.既不是轴对称图形也不是中心对称图形
(3)如图2,当0°<a<120°时,△ADE的周长是否会发生变化?若会变化,请说明理由,若不会变化,求出它的周长.
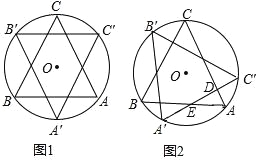
-
科目: 来源: 题型:
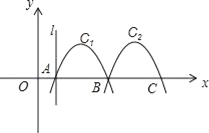
查看答案和解析>>【题目】如图,抛物线C1:y=x2+4x﹣3与x轴交于A、B两点,将C1向右平移得到C2,C2与x轴交于B、C两点.
(1)求抛物线C2的解析式.
(2)点D是抛物线C2在x轴上方的图象上一点,求S△ABD的最大值.
(3)直线l过点A,且垂直于x轴,直线l沿x轴正方向向右平移的过程中,交C1于点E交C2于点F,当线段EF=5时,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一个内角是80°,则它的底角是 0.
相关试题

