【题目】已知:如图,在△ABC中,∠C=90°,AE是△ABC的角平分线;ED平分∠AEB,交AB于点D;∠CAE=∠B.
(1)求∠B的度数.
(2)如果AC=3cm,求AB的长度.
(3)猜想:ED与AB的位置关系,并证明你的猜想.
参考答案:
【答案】
(1)解:∵AE是△ABC的角平分线,
∴∠CAE=∠EAB,
∵∠CAE=∠B,
∴∠CAE=∠EAB=∠B.
∵在△ABC中,∠C=90°,
∴∠CAE+∠EAB+∠B=3∠B=90°,
∴∠B=30°
(2)解:∵在△ABC中,∠C=90°,∠B=30°,AC=3cm,
∴AB=2AC=6cm
(3)解:猜想:ED⊥AB.理由如下:
∵∠EAB=∠B,
∴EB=EA,
∵ED平分∠AEB,
∴ED⊥AB
【解析】(1)根据角平分线定义和三角形内角和定理求出∠B的度数;(2)根据在直角三角形中,30度角所对的边是斜边的一半;求出AB的长度;(3)根据等腰三角形的性质,等角对等边得到EB=EA,根据三线合一得到ED⊥AB.
【考点精析】根据题目的已知条件,利用含30度角的直角三角形的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件服装标价500元,若以6折销售,仍可获利20%,则这件服装进价为______元.
-
科目: 来源: 题型:
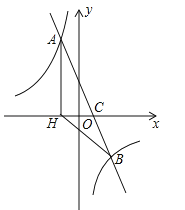
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数
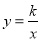 (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=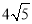 ,cos∠ACH=
,cos∠ACH=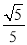 ,点B的坐标为(4,n)
,点B的坐标为(4,n)(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:
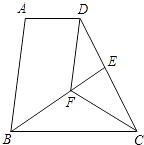
(1)△BFC≌△DFC;
(2)AD=DE. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
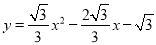 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.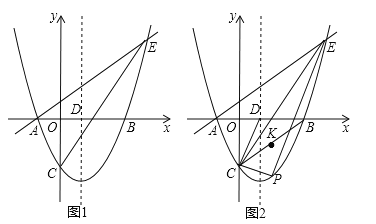
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线
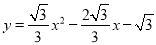 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
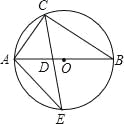
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A. 1:
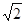 B. 1:
B. 1: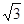 C. 1:2 D. 2:3
C. 1:2 D. 2:3
相关试题

