【题目】如图,在矩形ABCD中,AB=3,BC=5,以顶点B为圆心,边BC长为半径画弧,交AD边于点E,连结BE,过C点作CF⊥BE于F.
(1)求证:△ABE≌△FCB;
(2)求EF的长度.

参考答案:
【答案】(1)证明见解析;(2)EF=1
【解析】试题分析:(1)在由矩形ABCD中,AD∥BC,∠A=90°,易证得∠AEB=∠EBC,又由CF⊥BE,可得∠A=∠BFC=90°,然后由BE=BC,利用AAS即可判定△ABE≌△FCB;(2)利用勾股定理可求得AE的长,继而求得答案.
试题解析:(1)证明:在矩形ABCD中,AD∥BC,∠A=90°
∴∠AEB=∠EBC
∵CF⊥BE
∴∠BFC=90°
∴∠A=∠BFC=90°
∵BE=BC
∴△ABE≌△FCB(AAS)
(2)∵△ABE≌△FCB
∴AE=BF
在Rt△ABE中,AE=![]() ,
,
∴AE=BF =4
∴EF=BE-BF=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A.篮球 B.乒乓球C.羽毛球 D.足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,

请回答下列问题:
(1)这次被调查的学生共有多少人?
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若n为正整数,且a2n=3,计算(3a3n)2÷27a4n的值;
(2)已知(a-2)2+(b+2)2+(c-3)2=0,求
 a2b3c4·(3ab2c2)2÷6(a2b3c4)2的值.
a2b3c4·(3ab2c2)2÷6(a2b3c4)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
(1)若点D是AC的中点,求⊙P的半径AP的长;
(2)若AP=2,求CE的长;
(3)设线段BE的中点为Q,射线PQ与⊙P相交于点I,点P在运动的过程中,当点D、C、 I、P构成一个平行四边形时,请直接写出所有AP的长。
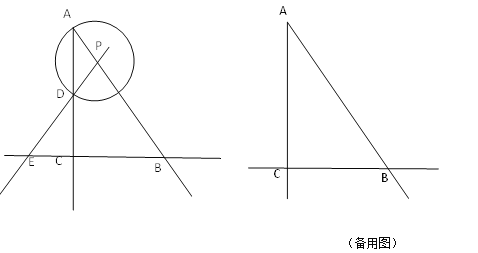
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解
(1)﹣x3+2x2y﹣xy2
(2)x2(x﹣2)+4(2﹣x)
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:9a3﹣ab2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】按如图方式摆放餐桌和椅子.用x来表示餐桌的张数,用y来表示可坐人数.
①题中有几个变量?
②你能写出两个变量之间的关系吗?

相关试题

