【题目】如图,以A(0, ![]() )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
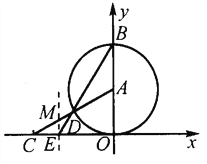
(1)分别求点E、C的坐标;
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心,ME为半径的圆与⊙A的位置关系,并说明理由.
参考答案:
【答案】(1)点C的坐标为(-3,0)(2)![]() (3)⊙M与⊙A外切
(3)⊙M与⊙A外切
【解析】试题分析:(1)已知了A点的坐标,即可得出圆的半径和直径,可在直角三角形BOE中,根据∠BEO和OB的长求出OE的长进而可求出E点的坐标,同理可在直角三角形OAC中求出C点的坐标;
(2)已知了对称轴的解析式,可据此求出C点关于对称轴对称的点的坐标,然后根据此点坐标以及C,A的坐标用待定系数法即可求出抛物线的解析式;
(3)两圆应该外切,由于直线DE∥OB,因此∠MED=∠ABD,由于AB=AD,那么∠ADB=∠ABD,将相等的角进行置换后可得出∠MED=∠MDE,即ME=MD,因此两圆的圆心距AM=ME+AD,即两圆的半径和,因此两圆外切.
试题解析:(1)在Rt△EOB中, ![]() ,
,
∴点E的坐标为(-2,0).
在Rt△COA中, ![]() ,
,
∴点C的坐标为(-3,0).
(2)∵点C关于对称轴![]() 对称的点的坐标为F(-1,0),
对称的点的坐标为F(-1,0),
点C与点F(-1,0)都在抛物线上.
设![]() ,用
,用![]() 代入得
代入得
![]() ,
,
∴![]() .
.
∴![]() ,即
,即
![]() .
.
(3)⊙M与⊙A外切,证明如下:
∵ME∥y轴,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴⊙M与⊙A外切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】组成多项式2x2﹣x﹣3的单项式是下列几组中的( )
A.2x2 , x,3
B.2x2 , ﹣x,﹣3
C.2x2 , x,﹣3
D.2x2 , ﹣x,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将P向右平移2个单位,再向下平移2个单位得点P′(-3,2),则点P的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
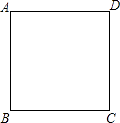
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果3xm+2y3与﹣2x3y2n﹣1是同类项,则m、n的值分别是( )
A.m=1,n=2
B.m=0,n=2
C.m=2,n=1
D.m=1,n=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线a平行于x轴,点M(-2,-3)是直线a上的一个点.若点N也是直线a上的一个点,MN=5,则点N的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种肥皂售价为每块2元,凡购买两块以上(含两块),商场推出两种优惠销售方法.第一种:“1块按原价,其余按原价的七折优惠”;第二种:“全部按原价的八折优惠”.你在购买相同数量的肥皂的情况下,要使第一种方法比第二种方法得到的优惠多,最少要购买肥皂( )块 .
A. 4B. 5C. 6D. 7
相关试题

