【题目】如图,数轴上点A,B表示到﹣2的距离都为6,P为线段AB上任一点,C,D两点分别从P,B同时向A点移动,且C点运动速度为每秒2个单位长度,D点运动速度为每秒3个单位长度,运动时间为t秒.
![]()
(1)A点表示数为 ,B点表示数为 ,AB= .
(2)若P点表示的数是0,
①运动1秒后,求CD的长度;
②当D在BP上运动时,求线段AC,CD之间的数量关系式.
参考答案:
【答案】(1)-8,4,12;(2)①3;②AC=2CD
【解析】
(1)根据两点间的距离公式即可求解;
(2)①根据路程=速度×时间得到C、D表示的数,再根据两点间的距离公式即可求解;
②分别表示出AC、CD,进一步得到线段AC、CD之间的数量关系式;
(1)A点表示数为﹣2﹣6=﹣8,B点表示的数为﹣2+6=4,AB=4﹣(﹣8)=12.
故答案为:﹣8,4,12;
(2)①运动1秒后,C:0﹣2×1=﹣2;D:4﹣3×1=1;
CD=1﹣(﹣2)=3;
②当D在BP上运动时,
AC=8﹣2t,CD=4﹣3t+2t=4﹣t,
则AC=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为充分发挥市场机制和价格杠杆在水资源配置中的作用,促进节约用水,提高用水效率,2017年7月1日起某地实行阶梯水价,价目如右表(注:水费按月结算,m3表示立方米):例:某户居民5月份共用水23m3,则应缴水费3×18+4×(23-18)=74(元).
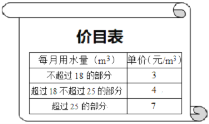
(1)若A居民家1月份共用水12m3,则应缴水费__________元;
(2)若B居民家2月份共缴水费66元,则用水__________m3;
(3)若C居民家3月份用水量为am3(a低于20m3,即a<20),且C居民家3、4两个月用水量共40m3,求3、4两个月共缴水费多少元?(用含a的代数式表示,不要求化简)
(4)在(3)中,当a=19时,求C居民家3、4两个月共缴水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=4
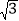 ,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.
,对角线AC、BD相交于点O,现将一个直角三角板OEF的直角顶点与O重合,再绕着O点转动三角板,并过点D作DH⊥OF于点H,连接AH.在转动的过程中,AH的最小值为_____.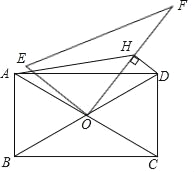
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.根据公司信息部的报告,yA、yB(万元)与投资金额x(万元)的部分对应值(如下表)

(1)求正比例函数和二次函数的解析式;
(2)如果公司准备投资20万元同时开发A、B两种新产品,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A(-1,1),B(-4,2),C(-3,4).
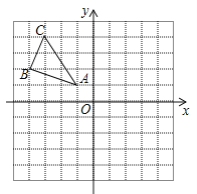
(1)在网格中画出△ABC向右平移5个单位后的图形△A1B1C1;
(2)在网格中画出△ABC关于原点O成中心对称后的图形△A2B2C2;
(3)请直接写出点B2、C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求
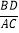 的值.
的值.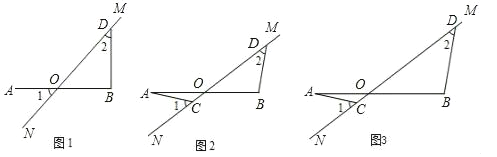
相关试题

