【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
参考答案:
【答案】
(1)解:∵A(1,3),B(4,0)在抛物线y=mx2+nx的图象上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x;
(2)解:存在三个点满足题意,理由如下:
当点D在x轴上时,如图1,过点A作AD⊥x轴于点D,

∵A(1,3),
∴D坐标为(1,0);
当点D在y轴上时,设D(0,d),则AD2=1+(3﹣d)2,BD2=42+d2,且AB2=(4﹣1)2+32=18,
∵△ABD是以AB为斜边的直角三角形,
∴AD2+BD2=AB2,即1+(3﹣d)2+42+d2=18,解得d=4,或d=﹣1
∴D点坐标为(0,4)或(0,﹣1);
综上可知存在满足条件的D点,其坐标为(1,0)或(0,4)或(0,﹣1);
(3)解:如图2,过P作PF⊥CM于点F,

∵PM∥OA,
∴Rt△ADO∽Rt△MFP,
∴ ![]() =
= ![]() =3,
=3,
∴MF=3PF,
在Rt△ABD中,BD=3,AD=3,
∴tan∠ABD=1,
∴∠ABD=45°,设BC=a,则CN=a,
在Rt△PFN中,∠PNF=∠BNC=45°,
∴tan∠PNF= ![]() =1,
=1,
∴FN=PF,
∴MN=MF+FN=4PF,
∵S△BCN=2S△PMN,
∴ ![]() a2=2×
a2=2× ![]() ×4PF2,
×4PF2,
∴a=2 ![]() PF,
PF,
∴NC=a=2 ![]() PF,
PF,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴MN= ![]() NC=
NC= ![]() a,
a,
∴MC=MN+NC=( ![]() +1)a,
+1)a,
∴M点坐标为(4﹣a,( ![]() +1)a),
+1)a),
又M点在抛物线上,代入可得﹣(4﹣a)2+4(4﹣a)=( ![]() +1)a,
+1)a,
解得a=3﹣ ![]() 或a=0(舍去),
或a=0(舍去),
OC=4﹣a= ![]() +1,MC=3+2
+1,MC=3+2 ![]() ,
,
∴点M的坐标为( ![]() +1,3+2
+1,3+2 ![]() ).
).
【解析】(1)利用待定系数法来求解;
(2)分两种情况来求解:点D在x轴上和点D在y轴上.当点D在x轴上时,过点A作AD⊥x轴于点D,易求D点的坐标;当点D在y轴上时,设D(0,d),,在Rt△ABD中利用勾股定理可求得d的值,课的答案;
(3)过P作PF⊥CM于点F,易证Rt△ADO∽Rt△MFP,从而得到MF=3PF,在Rt△ABD中和在Rt△PFN中利用三角函数得出MN=4PF,设BC=a,则CN=a,利用△BCN和△PMN之间的面积关系,进而表示出M的坐标,再根据M点在抛物线上求出a的值,进而得到答案.
【考点精析】根据题目的已知条件,利用勾股定理的概念和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D是BC的中点,CE⊥AD,垂足为点E,BF∥AC交CE的延长线于点F.
求证:AC=2BF.

-
科目: 来源: 题型:
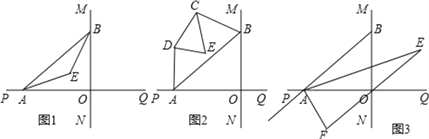
查看答案和解析>>【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△AOC是边长为2的等边三角形.
(1)写出△AOC的顶点C的坐标:_____.
(2)将△AOC沿x轴向右平移得到△OBD,则平移的距离是_____
(3)将△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是_____度
(4)连接AD,交OC于点E,求∠AEO的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
包场计费:包场每场每小时50元,每人须另付入场费5元
人数计费:每人打球2小时20元,接着续打球每人每小时6元
A. 9B. 8C. 7D. 6
相关试题

