搜索
【题目】如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角△ABC，使∠BAC＝90°，设点B的横坐标为x，则点C的纵坐标y与x的函数解析式是（ ）
A.y＝xB.y＝1﹣xC.y＝x+1D.y＝x﹣1
参考答案：
【答案】C
【解析】
过点C作CE⊥y轴于点E，只要证明△CEA≌△AOB（AAS），即可解决问题；
解：过点C作CE⊥y轴于点E．
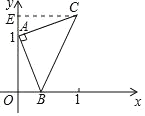
∵∠CEA＝∠CAB＝∠AOB＝90°，
∴∠EAC+∠OAB＝90°，∠OAB+∠OBA＝90°，
∴∠EAC＝∠ABO，
∵AC＝AB，
∴△CEA≌△AOB（AAS），
∴EA＝OB＝x，CE＝OA＝1，
∵C的纵坐标为y，OE＝OA+AD＝1+x，
∴y＝x+1．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上三点M，O，N对应的数分别为－1，0，3，点P为数轴上任意一点，其对应的数为x．
（1）MN的长为 ；
（2）如果点P到点M、点N的距离相等，那么x的值是 ；
（3）数轴上是否存在点P，使点P到点M、点N的距离之和是8？若存在，直接写出x的值；若不存在，请说明理由．
（4）如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动．设t分钟时点P到点M、点N的距离相等，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
A，B两种型号车的进货和销售价格如下表：
A型车
B型车
进货价格（元）
1 100
1 400
销售价格（元）
今年的销售价格
2 000
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】2022年将在北京﹣张家口举办冬季奥运会，很多学校开设了相关的课程．某校8名同学参加了冰壶选修课，他们被分成甲、乙两组进行训练，身高（单位：cm）如下表所示：
队员1
队员2
队员3
队员4
甲组
176
177
175
176
乙组
178
175
177
174
设两队队员身高的平均数依次为
，
，方差依次为S甲2，S乙2，下列关系中完全正确的是（ ）A.
＝，S甲2＜S乙2B.＝，S甲2＞S乙2C.
＜，S甲2＜S乙2D.＞，S甲2＞S乙2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB为⊙O的直径，点E在⊙O上，∠EAB的平分线交⊙O于点C，过点C作AE的垂线，垂足为D，直线DC与AB的延长线交于点P．
（1）判断直线PC与⊙O的位置关系，并说明理由；
（2）若tan∠P=
，AD=6，求线段AE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】窗户的形状如图所示（图中长度单位：cm），其中上部是半圆形，下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm.
（1）计算窗户的面积（计算结果保留π）.
（2）计算窗户的外框的总长（计算结果保留π）.
（3）安装一种普通合金材料的窗户单价是175元/平方米，当a=50cm时，请你帮助计算这个窗户安装这种材料的费用（π≈3.14，窗户面积精确到0.1）.
-
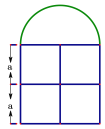
科目： 来源： 题型：
查看答案和解析>>【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合)，以CF为一边在等腰直角三角形外作正方形CDEF，连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α，得到如图2的情形。图2中BF交AC于点H，交AD于点O，请你判断（1）中得到的结论是否仍然成立，并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
相关试题
