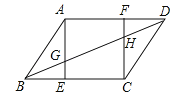
【题目】如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为E,F,AE,CF分别与BD交于点G和H,且AB=![]() .
.
(1)若tan∠ABE =2,求CF的长;
(2)求证:BG=DH.
参考答案:
【答案】(1)4;(2)证明见解析.
【解析】试题分析:(1)由平行四边形的性质,结合三角函数的定义,在Rt△CFD中,可求得CF=2DF,利用勾股定理可求得CF的长;
(2)利用平行四边形的性质结合条件可证得△AGD≌△CHB,则可求得BH=DG,从而可证得BG=DH.
试题解析:解:(1)解:∵四边形ABCD是平行四边形,∴∠CDF=∠ABE,DC=AB=![]() ,∵tan∠ABE=2,∴tan∠CDF=2,∵CF⊥AD,∴△CFD是直角三角形,∴
,∵tan∠ABE=2,∴tan∠CDF=2,∵CF⊥AD,∴△CFD是直角三角形,∴![]() =2,设DF=x,则CF=2x,在Rt△CFD中,由勾股定理可得(2x)2+x2=(
=2,设DF=x,则CF=2x,在Rt△CFD中,由勾股定理可得(2x)2+x2=(![]() )2,解得x=2或x=﹣2(舍去),∴CF=4;
)2,解得x=2或x=﹣2(舍去),∴CF=4;
(2)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠CBD,∵AE⊥BC,CF⊥AD,∴AE⊥AD,CF⊥BC,∴∠GAD=∠HCB=90°,∴△AGD≌△CHB,∴BH=DG,∴BG=DH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2700″=_____′=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(
 ),已知y与t之间的函数图象如图2所示.
),已知y与t之间的函数图象如图2所示.
给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②
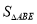 =48
=48 ;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.其中正确结论的序号是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式3(a2﹣2ab﹣b2)﹣(a2+mab+2b2)中不含有ab项,则m=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为极大地满足人民生活的需求,丰富市场供应,某区农村温棚设施农业迅速发展,温棚种植面积在不断扩大.在耕地上培成一行一行的长方形土埂,按顺序间隔种植不同农作物的方法叫分垄间隔套种.科学研究表明:在塑料温棚中分垄间隔套种高、矮不同的蔬菜和水果(同一种紧挨在一起种植不超过两垄),可增加它们的光合作用,提高单位面积的产量和经济效益.
现有一个种植总面积为540 m2的长方形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
占地面积(m2/垄)
产量(千克/垄)
利润(元/千克)
西红柿
30
160
1.1
草莓
15
50
1.6
(1)若设草莓共种植了
 垄,通过计算说明共有几种种植方案,分别是哪几种;
垄,通过计算说明共有几种种植方案,分别是哪几种;(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学七(2)班学生去劳动实践基地开展实践劳动,在劳动前需要分成x组,若每组11人,则余下一人,若每组12人,则有一组少4人,若每组分配7人,则该班可分成_____组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家商店将某种微波炉按原价提高20%后标价,又以9折优惠卖岀,结果每台微波炉比原价多赚了80元,这种微彼炉原价是_____元.
相关试题

