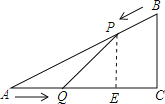
【题目】如图,在Rt△ABC中,AB=10cm,sinA=![]() .如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)
.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)

(1)求AC,BC的长;
(2)当t为何值时,△APQ的面积为△ABC面积的![]() ;
;
(3)当t为何值时,△APQ与△ABC相似.
参考答案:
【答案】(1)AC=8cm,BC=6cm;(2)当t为1s或4s时,△APQ的面积为△ABC面积的![]() ;(3)当t为
;(3)当t为![]() s或
s或![]() s时,△APQ与△ABC相似.
s时,△APQ与△ABC相似.
【解析】
试题分析:(1)根据正弦的定义和勾股定理求出AC,BC的长;
(2)作PE⊥AC于E,根据相似三角形的性质用t表示出PE,根据三角形的面积公式和题意列出方程,解方程即可;
(3)分△APQ∽△ABC和△APQ∽△ACB两种情况,根据相似三角形的性质列出方程,解方程即可.
解:(1)∵Rt△ABC中,AB=10cm,sinA=![]() ,
,
∴![]() =
=![]() ,
,
∴BC=6cm,
则AC=![]() =8cm,
=8cm,
∴AC=8cm,BC=6cm;
(2)作PE⊥AC于E,
由题意得,BP=2tcm,AQ=tcm,
则AP=(10﹣2t)cm,
∵PE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,PE=6﹣![]() t,
t,
∴△APQ的面积=![]() ×t×(6﹣
×t×(6﹣![]() t),△ABC面积=
t),△ABC面积=![]() ×6×8=24,
×6×8=24,
由题意得,![]() ×t×(6﹣
×t×(6﹣![]() t)=
t)=![]() ×24,
×24,
解得,t1=1,t2=4,
则当t为1s或4s时,△APQ的面积为△ABC面积的![]() ;
;
(3)当△APQ∽△ABC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
当△APQ∽△ACB时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
故当t为![]() s或
s或![]() s时,△APQ与△ABC相似.
s时,△APQ与△ABC相似.
-
科目: 来源: 题型:
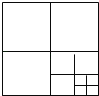
查看答案和解析>>【题目】连接边长为1的正方形对边中点,可将一个正方形分成四个全等的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成四个更小的小正方形,…重复这样的操作,则2004次操作后右下角的小正方形面积是( )
A.
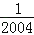 B.(
B.( )2004 C.(
)2004 C.(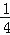 )2004 D.1﹣(
)2004 D.1﹣(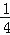 )2004
)2004 -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(﹣2a2)3=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠A和∠B的两边分别平行,且∠A比∠B的3倍少20°,则∠B的度数为( )
A. 10° B. 70° C. 10°或50° D. 70°或50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=30°+∠B,则∠B=____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角都是140°,则这个多边形是___边形,它的内角和是___°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解方程
(1)(3
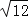 +2
+2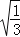 ﹣
﹣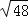 )÷2
)÷2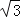
(2)0.259×49+π0+(﹣22)3+(
 )﹣2
)﹣2(3)(x﹣3y)(2x+3y)﹣(x﹣3y)(x+3y)
(4)解方程:
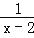 =
=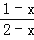 ﹣2.
﹣2.
相关试题

