【题目】已知一元二次方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求![]() 的取值范围;
的取值范围;
(2)如果![]() 是符合条件的最大整数,且一元二次方程
是符合条件的最大整数,且一元二次方程![]() 与
与![]() 有一个相同的根,求此时
有一个相同的根,求此时![]() 的值.
的值.
参考答案:
【答案】解:(1)k![]() 4;
4;
(2)m=![]()
【解析】试题分析:(1)根据方程有两个不等实数根,可得判别式大于零,根据解不等式,可得答案;
(2)根据解方程,可得x2﹣4x+k=0的解,根据解相同,把方程的解代入,可得关于m的一元一次方程,根据解一元一次方程,可得答案.
试题解析:(1)由一元二次方程x2﹣4x+k=0有两个不相等的实数根,得
△=b2﹣4ac=(﹣4)2﹣4k>0,
解得k<4;
(2)由k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0,得
x2﹣4x+3=0,
解得x1=1,x2=3,
一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,
当x=1时,把x=1代入x2+mx﹣1=0,得1+m﹣1=0,解得m=0,
当x=3时,把x=3代入x2+mx﹣1=0,得9+3m﹣1=0,解得![]() ,
,
综上所述:如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,m=0或![]() .
.
-
科目: 来源: 题型:
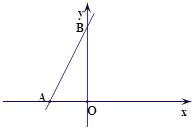
查看答案和解析>>【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
 (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.(1)求点A、B、D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2y)2(﹣3y)+(4y5)÷2y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了选拔学生参加我市2011年无线电测向比赛中的装机比赛,教练对甲、乙两选手平时五次训练成绩进行统计,两选手五次训练的平均成绩均为30分钟,方差分别是S甲2=51、S乙2=12.则甲、乙两选手成绩比较稳定的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植-亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店经销一批小商品,每件商品的成本为8元.据市场分析,销售单价定为10元时,每天能售出200件;现采用提高商品售价,减少销售量的办法增加利润,若销售单价每涨1元,每天的销售量就减少20件.
设销售单价定为x元.据此规律,请回答:
(1)商店日销售量减少___________件,每件商品盈利___________元(用含x的代数式表示);
(2)针对这种小商品的销售情况,该商店要保证每天盈利640元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 (k为常数).
(k为常数).(1)k为何值时,该函数是正比例函数;
(2)k为何值时,正比例函数过第一、三象限,写出正比例函数解析式;
(3)k为何值时,正比例函数y随x的增大而减小,写出正比例函数的解析式.
相关试题

