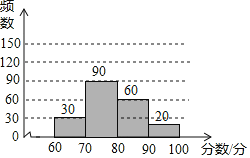
【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?

参考答案:
【答案】(1)200、90、0.3;(2)详见解析;(3)54°;(4)240.
【解析】
(1)根据60≤x<70的频数及其频率求得总人数,进而计算可得m、n的值;(2)根据(1)的结果,可以补全直方图;(3)用360°乘以样本中分数段60≤x<70的频率即可得;(4)总人数乘以样本中成绩80≤x<100范围内的学生人数所占比例.
(1)本次调查的总人数为30÷0.15=200人,
则m=200×0.45=90,n=60÷200=0.3,
故答案为:200、90、0.3;
(2)补全频数分布直方图如下:
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是360°×0.15=54°,
故答案为:54°;
(4)600×![]() =240,
=240,
答:估计该校成绩80≤x<100范围内的学生有240人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.

(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF;②∠AEF=45°;③S四边形EFHG=S△DEF+S△AGH;④△AEF≌△CDE

其中正确的结论有______ (填正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D在边BA或BA的延长线上,过点D作DE∥BC,交∠ABC的角平分线于点E.
(1)如图1,当点D在边BA上时,点E恰好在边AC上,求证:∠ADE=2∠DEB;
(2)如图2,当点D在BA的延长线上时,请直接写出∠ADE与∠DEB之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;

(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是 .

相关试题

