搜索
【题目】为了方便居民低碳出行，聊城市公共自行车租赁系统（一期）试运行．图①是公共自行车的实物图，图②是公共自行车的车架示意图，点A、D、C、E在同一条直线上，CD=30cm，DF=20cm，AF=25cm，FD⊥AE于点D，座杆CE=15cm，且∠EAB=75°．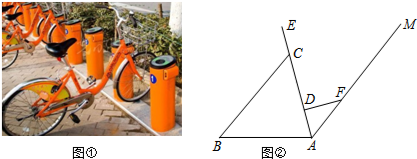 
（1）求AD的长；
（2）求点E到AB的距离．（精确到0.1cm，参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）
参考答案：
【答案】
（1）解：在Rt△ADF中，由勾股定理得，
AD= 
= 
=15（cm）
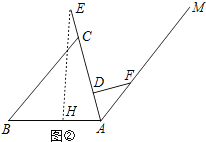
（2）解：AE=AD+CD+EC=15+30+15=60（cm），
如图②，过点E作EH⊥AB于H，
在Rt△AEH中，sin∠EAH= 
，
则EH=AEsin∠EAH=ABsin75°≈60×0.97=58.2（cm）．
答：点E到AB的距离为58.2 cm．
【解析】（1）根据勾股定理求出AD的长；（2）作EH⊥AB于H，求出AE的长，根据正弦的概念求出点E到车架AB的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC⊥CD，∠BED＝90°.填空：
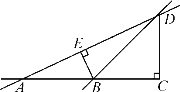
(1)∠ACD＝_____度；
(2)直线AD与BE的位置关系是__________；
(3)点B到直线AD的距离是线段________的长度，点D到直线AB的距离是线段______的长度；
(4)在线段DA，DB，DC中，最短的是线段______；在线段BA，BE，BD中，最短的是线段______，理由是_____________________________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．
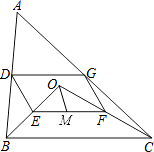
（1）求证：四边形DEFG是平行四边形；
（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】（7分）如图所示，O是直线AB上一点，∠AOC=
∠BOC，OC是∠AOD的平分线．
（1）求∠COD的度数．
（2）判断OD与AB的位置关系，并说出理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】黔东南州某中学为了解本校学生平均每天的课外学习实践情况，随机抽取部分学生进行问卷调查，并将调查结果分为A，B，C，D四个等级，设学生时间为t（小时），A：t＜1，B：1≤t＜1.5，C：1.5≤t＜2，D：t≥2，根据调查结果绘制了如图所示的两幅不完整的统计图．
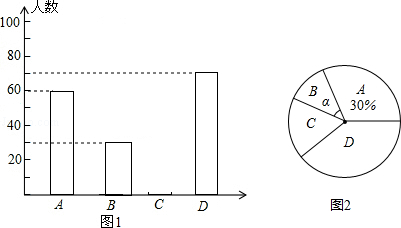
请你根据图中信息解答下列问题：
（1）本次抽样调查共抽取了多少名学生？并将条形统计图补充完整；
（2）本次抽样调查中，学习时间的中位数落在哪个等级内？
（3）表示B等级的扇形圆心角α的度数是多少？
（4）在此次问卷调查中，甲班有2人平均每天课外学习时间超过2小时，乙班有3人平均每天课外学习时间超过2小时，若从这5人中任选2人去参加座谈，试用列表或化树状图的方法求选出的2人来自不同班级的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】为满足市场需求，新生活超市在端午节前夕购进价格为3元/个的某品牌粽子，根据市场预测，该品牌粽子每个售价4元时，每天能出售500个，并且售价每上涨0.1元，其销售量将减少10个，为了维护消费者利益，物价部门规定，该品牌粽子售价不能超过进价的200%，请你利用所学知识帮助超市给该品牌粽子定价，使超市每天的销售利润为800元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（
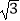，1）在反比例函数y= 
的图象上．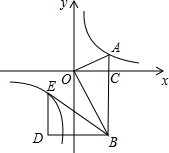
（1）求反比例函数y= 的表达式；
（2）在x轴的负半轴上存在一点P，使得S△AOP=
S△AOB ， 求点P的坐标；
（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上．
相关试题
