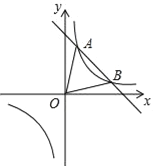
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出不等式kx+b﹣![]() >0的解集;
>0的解集;
(3)若点M在x轴上、点N在y轴上,且以M、N、A、B为顶点的四边形是平行四边形,请直接写出点M、N的坐标.
参考答案:
【答案】(1)反比例函数解析为y=![]() ,一次函数解析式为y=﹣2x+8;(2)解集为1<x<3或x<0;(3)以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).
,一次函数解析式为y=﹣2x+8;(2)解集为1<x<3或x<0;(3)以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).
【解析】试题分析:(1)由A点坐标可求得m的值,可求得反比例函数解析式,则可求得B点坐标,由A、B两点坐标,利用待定系数法可求得直线AB的解析式;
(2)结合函数图象可知不等式的解集即为一次函数图象在反比例函数图象上方时对应的x的取值范围,结合A、B坐标可求得答案;
(3)当AB为平行四边形的边时,①当M在x轴正半轴,N在y轴正半轴时,过A作AC∥y轴,过B作BC∥x轴,可证明△ABC≌△NMO,则可求得OM和ON,②当M在x轴负半轴,N在y轴负半轴时,同理可求得OM和ON的长,则可求得M、N的坐标;当AB为对角线时,可求得M、N、A、B四点共线,不合题意.
试题解析:(1)反比例函数y=![]() 的图象过A(1,6),
的图象过A(1,6),
∴m=1×6=6,
∴反比例函数解析为y=![]() ,
,
把x=3代入可得n=2,
∴B(3,2),
设直线AB解析式为y=kx+b,
把A、B坐标代入可得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣2x+8;
(2)不等式kx+b﹣![]() >0可化为不等式kx+b>
>0可化为不等式kx+b>![]() ,
,
即直线在反比例函数图象上方时所对应的自变量x的取值范围,
∵A(1,6),B(3,2),
∴不等式kx+b﹣![]() >0的解集为1<x<3或x<0;
>0的解集为1<x<3或x<0;
(3)当AB为平行四边形的边时,
①当M在x轴正半轴,N在y轴正半轴时,如图1,过A作AC∥y轴,过B作BC∥x轴,
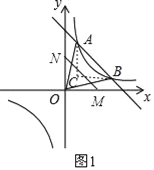
∵A(1,6),B(3,2),
∴BC=3﹣1=2,AC=6﹣2=4,
∵MN∥AB,且MN=AB,
∴∠ONM=∠CAB,
在△NOM和△ACB中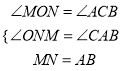 ,
,
∴△NOM≌△ACB(AAS),
∴OM=BC=2,ON=AC=4,
∴M(2,0),N(0,4);
②当M在x轴的负半轴、N在y轴的负半轴时,同理可求得M(﹣2,0),N(0,﹣4);
当AB为对角线时,设M(x,0),N(0,y),
∵A(1,6),B(3,2),
∴平行四边形的对称中心为(2,4),
∴x+0=4,y+0=8,解得x=4,y=8,此时M(4,0),N(0,8),
在y=﹣2x+8中,令y=0可得x=4,令x=0可得y=8,
∴A、B、M、N四点共线,不合题意,舍去;
综上可知以M、N、A、B为顶点的四边形是平行四边形时,M(﹣2,0),N(0,﹣4)或M(4,0),N(0,8).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
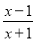 ,
, 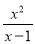 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 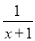 ,
, 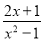 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 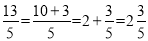 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
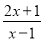 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
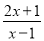 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
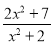 的最大值为 .
的最大值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
-
科目: 来源: 题型:
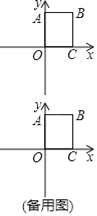
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣5x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】单位举行歌咏比赛,分两场举行,第一场8名参赛选手的平均成绩为88分,第二场4名参赛选手的平均成绩为94分,那么这12名选手的平均成绩是____分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(3a2﹣a﹣1)﹣2(3﹣a+2a2),其中a=2.
相关试题

