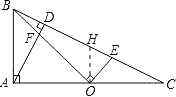
【题目】如图(1),在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上的一点,连接BO交AD于点F,OE⊥OB交BC边于点E.
(1)试说明:△ABF∽△COE.
(2)如图(2),当O为AC边的中点,且![]() 时,求
时,求![]() 的值.
的值.
(3)当O为AC边的中点,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

参考答案:
【答案】![]() 详见解析;
详见解析; ![]() (3)
(3)![]()
【解析】
(1)要求证:△ABF∽△COE.只要证明∠BAF=∠C,∠ABF=∠COE即可.
(2)作![]() 交BC于H,易证:△OEH∽△OFA,根据相似三角形的对应边的比相等,即可得出所求的值.同理可得(3)
交BC于H,易证:△OEH∽△OFA,根据相似三角形的对应边的比相等,即可得出所求的值.同理可得(3)![]()
(1)证明:∵AD⊥BC,
∴![]()
∵![]()
∴∠BAF=∠C.
∵OE⊥OB,
∴![]()
∵![]()
∴∠ABF=∠COE.
∴△ABF∽△COE.
(2)过O作AC垂线交BC于H,则OH![]() AB,
AB,
由(1)得∠ABF=∠COE,∠BAF=∠C.
∴∠AFB=∠OEC,
∴∠AFO=∠HEO,
而∠BAF=∠C,
∴∠FAO=∠EHO,
∴△OEH∽△OFA,
∴OF:OE=OA:OH
又∵O为AC的中点,OH![]() AB.
AB.
∴OH为△ABC的中位线,
∴![]()
而![]()
∴OA:OH=2:1,
∴OF:OE=2:1,即![]()
(3)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形。用A种纸片张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1____________;方法2_____________;
(2)观察图2,请你直接写出下列三个代数式: (a+b)
 , a
, a +b
+b ,ab之间的等量关系_____________;
,ab之间的等量关系_____________;(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a
 +3ab+2b
+3ab+2b ;
;(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6, a
 +b
+b =14,求ab的值;
=14,求ab的值;②已知(x2018)
 +(x2020)
+(x2020) =34,求(x2019)
=34,求(x2019) 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.

(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由. -
科目: 来源: 题型:
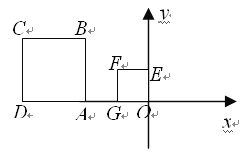
查看答案和解析>>【题目】(11·贵港)如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标
为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是 _ ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )

A.
 B.
B. 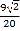 C.
C.  D.
D. 
-
科目: 来源: 题型:
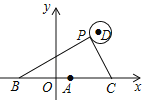
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
 根据表、图提供的信息,解决以下问题:
根据表、图提供的信息,解决以下问题:(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
相关试题

