【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
过F作FH⊥AD于H,交ED于O,于是得到FH=AB=2,根据勾股定理得到AF=![]() =
=![]() =
=![]() ,根据平行线分线段成比例定理得到,OH=
,根据平行线分线段成比例定理得到,OH=![]() AE=
AE=![]() ,由相似三角形的性质得到
,由相似三角形的性质得到![]() =
=![]() ,求得AM=
,求得AM=![]() AF=
AF=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,求得AN=
,求得AN=![]() AF=
AF=![]() ,即可得到结论.
,即可得到结论.
过F作FH⊥AD于H,交ED于O,则FH=AB=2.
∵BF=2FC,BC=AD=3,
∴BF=AH=2,FC=HD=1,
∴AF=![]() =
=![]() =
=![]() ,
,
∵OH∥AE,
∴![]() =
=![]() ,
,
∴OH=![]() AE=
AE=![]() ,
,
∴OF=FH﹣OH=2﹣![]() =
=![]() ,
,
∵AE∥FO,∴△AME∽△FMO,
∴![]() =
=![]() ,∴AM=
,∴AM=![]() AF=
AF=![]() ,
,
∵AD∥BF,∴△AND∽△FNB,
∴![]() =
=![]() ,
,
∴AN=![]() AF=
AF=![]() ,
,
∴MN=AN﹣AM=![]() ﹣
﹣![]() =
=![]() ,故选B.
,故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=6,点E是边CD上的动点(点E不与端点C,D重合),AE的垂直平分线FG分别交AD,AE,BC于点F,H,G.当
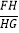 =
=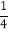 时,DE的长为( )
时,DE的长为( )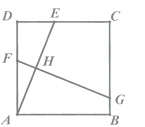
A. 2 B.
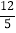 C.
C. 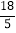 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点D在
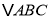 的AB边上,且
的AB边上,且 .
.
(1)作
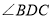 的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,判断直线DE与直线AC的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某湖上风景区有两个观望点A,C和两个度假村B、D;度假村D在C正西方向,度假村B在C的南偏东
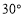 方向,度假村B到两个观望点的距离都等于2km.
方向,度假村B到两个观望点的距离都等于2km.(1)在图中标出A、B、C、D的位置,并写出道路CD与CB的夹角.
(2)如果度假村D到C是直公路,长为1km,D到A是环湖路,度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程.求出环湖路的长.
(3)根据题目中的条件,能够判定
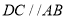 吗?若能,请写出判断过程;若不能,请你添加一个条件,判定
吗?若能,请写出判断过程;若不能,请你添加一个条件,判定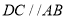 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某个函数给定如下定义:若存在实数M>0,对于任意的函数值y,都满足|y|≤M,则称这个函数是有界函数.在所有满足条件的M中,其中最小值称为这个函数的边界值.现将有界函数y=2
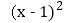 +1(0
+1(0 x
x m,1≤m≤2)的图象向下平移m个单位,得到的函数边界值是t,且
m,1≤m≤2)的图象向下平移m个单位,得到的函数边界值是t,且 ≤t≤2,则m的取值范围是( )
≤t≤2,则m的取值范围是( )A. 1≤m≤
 B.
B.  ≤m≤
≤m≤ C.
C.  ≤m≤
≤m≤ D.
D.  ≤m≤2
≤m≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果
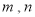 是两个不相等的实数,且满足
是两个不相等的实数,且满足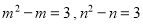 ,那么代数式
,那么代数式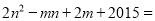 _____.
_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,2)关于直线y=k
 (k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
(k>0)的对称点恰好落在x轴的正半轴上,则k的值是_____.
相关试题

