【题目】一个三位正整数M,其各位数字均不为零且互不相等.若将M的十位数字与百位数字交换位置,得到一个新的三位数,我们称这个三位数为M的“友谊数”,如:168的“友谊数”为“618”;若从M的百位数字、十位数字、个位数字中任选两个组成一个新的两位数,并将得到的所有两位数求和,我们称这个和为M的“团结数”,如:123的“团结数”为12+13+21+23+31+32=132.
(1)求证:M与其“友谊数”的差能被15整除;
(2)若一个三位正整数N,其百位数字为2,十位数字为a、个位数字为b,且各位数字互不相等(a≠0,b≠0),若N的“团结数”与N之差为24,求N的值.
参考答案:
【答案】(1)答案见解析;(2)284或218.
【解析】整体分析:
(1)M为100a+10b+c,计算M与其“友谊数”的差;(2)用N的“团结数”与N之差为24列方程,结合a,b是正整数求解.
解:(1)由题意可得,
设M为100a+10b+c,则它的友谊数为:100b+10a+c,
(100a+10b+c)﹣(100b+10a+c)
=100a+10b+c﹣100b﹣10a﹣c
=100(a﹣b)+10(b﹣a)
=90(a﹣b),
∵![]() =6(a-b),
=6(a-b),
∴M与其“友谊数”的差能被15整除;
(2)由题意可得,
N=2×100+10a+b=200+10a+b,
N的团结数是:10×2+a+10a+2+10×2+b+10×b+2+10a+b+10b+a=22a+22b+44,
∴22a+22b+44﹣(200+10a+b)=24,
解得, ![]() 或
或![]() .
.
即N是284或218.
-
科目: 来源: 题型:
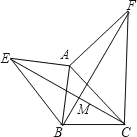
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
求证:(1)EC=BF;(2)EC⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,一个多边形的每一个外角都是它相邻的内角的
 .试求出:(1)这个多边形的每一个外角的度数;(2)求这个多边形的内角和.
.试求出:(1)这个多边形的每一个外角的度数;(2)求这个多边形的内角和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=80°,AD是BC边上的高,AE平分∠BAC.
(1)求∠BAE的度数;(2)求∠DAE的度数.

-
科目: 来源: 题型:
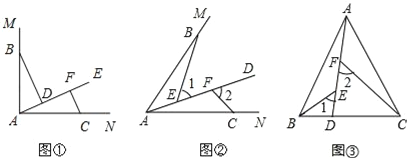
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
-
科目: 来源: 题型:
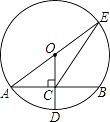
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2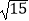
B.8
C.2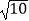
D.2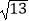
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠CDB′等于( )

A.40°
B.60°
C.70°
D.80°
相关试题

