【题目】在△ABC中,![]() ,
,![]() 边上的高
边上的高![]() ,则边
,则边![]() 的长为( )
的长为( )
A. 4 B. 14 C. 4 或14 D. 8或14
参考答案:
【答案】C
【解析】
分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=BD﹣CD.
(1)如图1,锐角△ABC中,AB=15,AC=13,BC边上高AD=12.在Rt△ABD中AB=15,AD=12,由勾股定理得:BD2=AB2﹣AD2=152﹣122=81,则BD=9.在Rt△ACD中AC=13,AD=12,由勾股定理得:CD2=AC2﹣AD2=132﹣122=25,则CD=5,故BC的长为BD+DC=9+5=14;
(2)如图2,钝角△ABC中,AB=15,AC=13,BC边上高AD=12.在Rt△ABD中AB=15,AD=12,由勾股定理得:BD2=AB2﹣AD2=152﹣122=81,则BD=9.在Rt△ACD中AC=13,AD=12,由勾股定理得:CD2=AC2﹣AD2=132﹣122=25,则CD=5,故BC的长为BD﹣CD=9﹣5=4.
综上可得BC的长为14或4.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形,BE、CD相交于点F.求证:AF⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
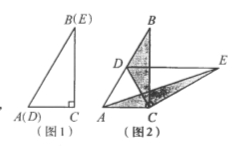


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 分别在
分别在 上,且
上,且 ,点
,点 分别在
分别在 上运动,则
上运动,则 的最小值为______。
的最小值为______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A按顺时针方向旋转到△AB1C1的位置,点B1恰好落在边BC的中点处.那么旋转的角度等于( )

A.55°
B.60°
C.65°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.

相关试题

