
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 为对角线
为对角线![]() 的中点.
的中点.
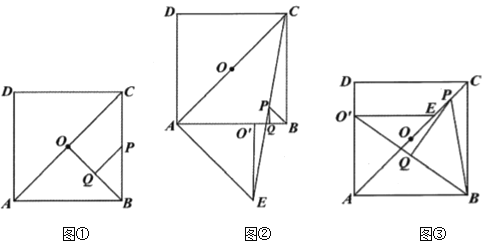
(1)问题解决:如图①,连接![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 的数量关系是_____,位置关系是____;
的数量关系是_____,位置关系是____;
(2)问题探究:如图②,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .判断
.判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)拓展延伸:如图③,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .若正方形
.若正方形![]() 的边长为1,求
的边长为1,求![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的形状是等腰直角三角形,理由见解析;(3)
的形状是等腰直角三角形,理由见解析;(3)![]()
【解析】
(1)根据题意可得PQ为△BOC的中位线,再根据中位线的性质即可求解;
(2)连接![]() 并延长交
并延长交![]() 于点
于点![]() ,根据题意证出
,根据题意证出![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 也为等腰直角三角形,由
也为等腰直角三角形,由![]() 且
且![]() 可得
可得![]() 是等腰直角三角形;
是等腰直角三角形;
(3)延长![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,
,![]() .证出四边形
.证出四边形![]() 是矩形,
是矩形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,再证出
,再证出![]() 为等腰直角三角形,根据图形的性质和勾股定理求出O′A,O′B和BQ的长度,即可计算出
为等腰直角三角形,根据图形的性质和勾股定理求出O′A,O′B和BQ的长度,即可计算出![]() 的面积.
的面积.
解:(1)∵点P和点Q分别为![]() ,
,![]() 的中点,
的中点,
∴PQ为△BOC的中位线,
∵四边形![]() 是正方形,
是正方形,
∴AC⊥BO,
∴![]() ,
,![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)![]() 的形状是等腰直角三角形.理由如下:
的形状是等腰直角三角形.理由如下:
连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,
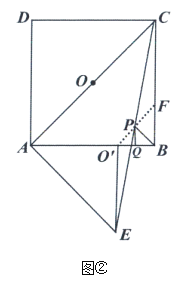
由正方形的性质及旋转可得![]() ,∠
,∠![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
又∵点![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,∴
,∴![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]() ,
,![]() .
.
∴![]() 也为等腰直角三角形.
也为等腰直角三角形.
又∵点![]() 为
为![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
∴![]() 的形状是等腰直角三角形.
的形状是等腰直角三角形.
(3)延长![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,
,![]() .
.
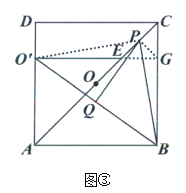
∵四边形![]() 是正方形,
是正方形,![]() 是对角线,
是对角线,
∴![]() .
.
由旋转得,四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交,其中一个交点的横坐标是2.
的图象相交,其中一个交点的横坐标是2.
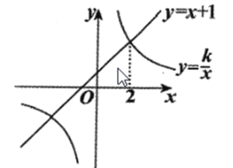
(1)求反比例函数的表达式;
(2)将一次函数![]() 的图象向下平移2个单位,求平移后的图象与反比例函数
的图象向下平移2个单位,求平移后的图象与反比例函数![]() 图象的交点坐标;
图象的交点坐标;
(3)直接写出一个一次函数,使其过点![]() ,且与反比例函数
,且与反比例函数![]() 的图象没有公共点.
的图象没有公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区统计了有扶贫任务的人员一个月下乡扶贫的天数(为整数),并制成了如下尚不完整的表格与条形统计图(如图).
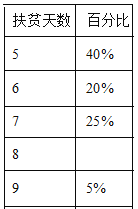
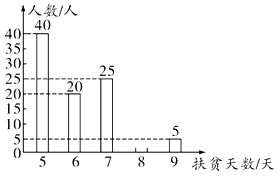
(1)有扶贫任务的人员的总人数是__________,并补全条形统计图;
(2)上级部门随机抽查1名扶贫人员,检查其工作情况,求抽查到的扶贫人员的扶贫天数大于7天的概率;
(3)若统计时漏掉1名扶贫人员,现将他的下乡天数和原统计的下乡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名扶贫人员下乡的天数最少是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
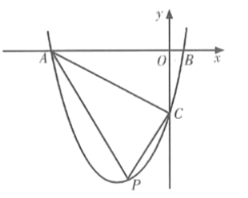
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 是第三象限内抛物线上的一动点.
是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象
的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)当![]() 的顶点在
的顶点在![]() 上时,求
上时,求![]() 的值;
的值;
(2)若![]() 、
、![]() 两点中有一点与点
两点中有一点与点![]() 关于原点对称,试判断这个点是点
关于原点对称,试判断这个点是点![]() 还是点
还是点![]() ;
;
(3)若![]() 的顶点为
的顶点为![]() ,对称轴与
,对称轴与![]() 的交点为
的交点为![]() ,且点
,且点![]() 在点
在点![]() 的下方,当
的下方,当![]() 为何值时,线段
为何值时,线段![]() 的长最大.
的长最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com