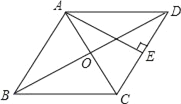
【题目】如图,已知菱形ABCD对角线交于点O,AE⊥CD于E,AE=OD,则∠CAE=_____.
参考答案:
【答案】30°
【解析】分析:由四边形ABCD为菱形,得到对角线互相垂直,进而得到一对直角相等,再由对顶角相等,得到△AFO与△DFE相似,利用相似三角形对应角相等得到一对角相等,利用ASA得到△AEC与△DOC全等,利用全等三角形对应边相等得到AC=CD,进而确定出△ACD为等边三角形,利用等边三角形的性质及三线合一性质即可求出所求角的度数.
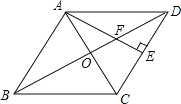
详解:∵菱形ABCD, ∴AC⊥BD,AD=DC, ∵AE⊥CD, ∴∠AEC=∠DOC=90°,
∵∠AOD=∠AED=90°,∠AFO=∠DFE, ∴△AFO∽△DFE, ∴∠CAE=∠CDO,
∴△AEC≌△DOC(ASA), ∴AC=CD, ∴AC=CD=AD,即△ACD为等边三角形,
∵AE⊥CD, ∴AE为∠CAD的平分线, 则∠CAE=30°. 故答案为:30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
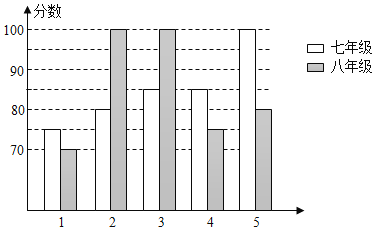
(1)根据所给信息填写表格;
平均数(分)
中位数(分)
众数(分)
七年级
85
八年级
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=10,AB=14,点E为DC上一个动点,若将△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,则点D′到AB的距离为( )

A. 6 B. 6或8 C. 7或8 D. 6或7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知A(
 ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A.(
 ,0) B.(1,0) C.(
,0) B.(1,0) C.( ,0) D.(
,0) D.( ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】附加题:(y﹣z)2+(x﹣y)2+(z﹣x)2=(y+z﹣2x)2+(z+x﹣2y)2+(x+y﹣2z)2.
求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两条直线AB,CD相交于点O,且∠AOC=∠AOD,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s,运动时间为t秒(0<t<12,本题出现的角均小于平角)
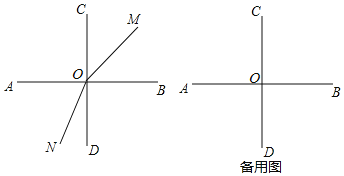
(1)图中一定有 个直角;当t=2时,∠MON的度数为 ,∠BON的度数为 ;
(2)若OE平分∠COM,OF平分∠NOD,当∠EOF为直角时,请求出t的值;
(3)当射线OM在∠COB内部,且
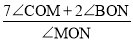 是定值时,求t的取值范围,并求出这个定值.
是定值时,求t的取值范围,并求出这个定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果的价格如表:
购买的质量(千克)
不超过10千克
超过10千克
每千克价格
6元
5元
张欣两次共购买了25千克这种水果(第二次多于第一次),共付款132元.问张欣第一次、第二次分别购买了多少千克这种水果?
相关试题

