【题目】如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E. 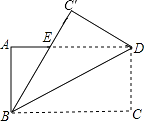
(1)判断△EBD的形状,并说明理由;
(2)求DE的长.
参考答案:
【答案】
(1)证明:∵△BDC1是由△BDC沿直线BD折叠得到的,
∴∠C1BD=∠CBD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBD=∠EDB,
∴∠C1BD=∠EDB,
∴BE=DE,
∴△EBD是等腰三角形;
(2)解:设DE=x,则AE=AD﹣DE=8﹣x,
∵∠A=90°,BE=DE=x,
在Rt△ABE中,BE2=AB2+AE2,
∴x2=62+(8﹣x)2,
∴x= ![]() ,
,
即DE= ![]() .
.
【解析】(1)因为折叠前后∠DBC=∠DBC1,且平行,内错角相等,所以∠DCB=∠DAB,所以根据角之间的等量代换可得∠C1BD=∠EDB,根据等边对等角可知DE=BE;(2)设DE=x,则AE=AD﹣DE=8﹣x,在Rt△ABE中,根据勾股定理得:BE2=AB2+AE2,然后代入各值求解即可.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile
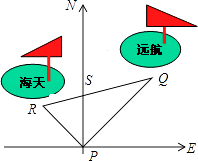
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形的两边长为6和9,则第三边长可能是( )
A.16B.15C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
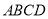 内接于
内接于 ,
, 是
是 的直径,点
的直径,点 在
在 的延长线上,
的延长线上, .
.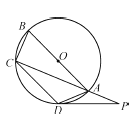
(Ⅰ)若
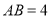 ,求弧
,求弧 的长;
的长;(Ⅱ)若弧
 弧
弧 ,
, ,求证:
,求证: 是
是 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D,E分别在边BC 和AC上,若AD=AE,则下列结论错误的是( )
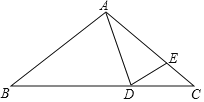
A.∠ADB=∠ACB+∠CAD B.∠ADE=∠AED
C.∠CDE=
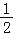 ∠BAD D.∠AED=2∠ECD
∠BAD D.∠AED=2∠ECD -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.全等三角形的周长相等B.全等三角形的对应角相等
C.全等三角形的面积相等D.面积相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.0是最小的整数
B.最大的负整数是﹣1
C.任何有理数的绝对值都是正数
D.一个有理数的平方总是正数
相关试题

