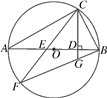
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
参考答案:
【答案】证明见解析.
【解析】试题分析:要证明BC2=BG·BF即要证明△BCG∽△BFC,已知∠GBC=∠CBF,即要证明∠BCG=∠F,由于∠F=∠A,即要证明∠A=∠BCG,由已知条件不难证明.
试题解析:
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵CD⊥AB于点D,
∴∠ACD+∠A=90°,
∴∠BCD=∠A.
又∵∠A=∠F,
∴∠F=∠BCD=∠BCG.
在△BCG和△BFC中,
∵![]() ,
,
∴△BCG∽△BFC.
∴![]() =
=![]() ,
,
即BC2=BG·BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某造纸厂为了保护环境,准备购买A,B两种型号的污水处理设备共6台,用于同时治理不同成分的污水,若购买A型2台,B型3台需54万元,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水180吨,如果该企业每月的污水处理量不低于1150吨,问共有几种购买方案?请你为该企业设计一种最省钱的购买方案并求此时的购买费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分6分)
(1)(3分)(-3)2-|-
 |+(3.14-x)0
|+(3.14-x)0(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的
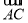 、
、 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.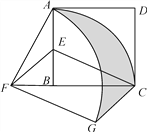
-
科目: 来源: 题型:
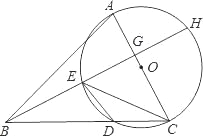
查看答案和解析>>【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
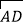 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
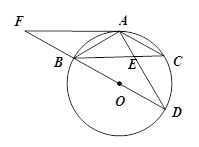
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
相关试题

