【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
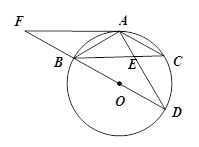
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
参考答案:
【答案】

【解析】试题分析:(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
(1)证明:∵AB=AC,
∴∠ABC=∠C(等边对等角),
∵∠C=∠D(同弧所对的圆周角相等),
∴∠ABC=∠D(等量代换),
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
(2)解:∵△ABE∽△ADB,
∴![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=.
(3)解:直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴![]() =4
=4
BF=BO=![]() ,
,
∵AB=,
∴BF=BO=AB,
∴∠OAF=90°,
∴OA⊥AF,
∵AO是圆的半径,
∴直线FA与⊙O相切.
-
科目: 来源: 题型:
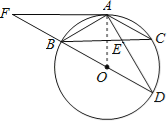
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的
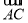 、
、 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.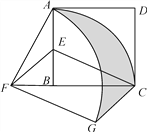
-
科目: 来源: 题型:
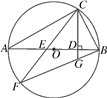
查看答案和解析>>【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
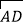 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米.图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.
(1)搅匀后从中随机摸出一球,请直接写出摸出红球的概率;
(2)如果第一次随机摸出一个球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
相关试题

