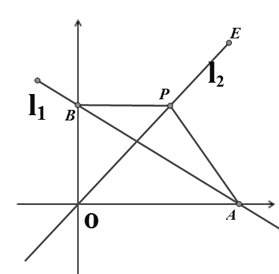
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 经过
经过![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 满足
满足![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() :
:![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)点![]() 是
是![]() 轴上的一个动点,点
轴上的一个动点,点![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 是等腰直角三角形,请直接写出符合条件的
是等腰直角三角形,请直接写出符合条件的![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)存在点
;(2)存在点![]() ,
,![]() 点的纵坐标为0或4;(3)4或
点的纵坐标为0或4;(3)4或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据非负性求出a、b的值,然后运用待定系数法解答即可;
(2)根据平行和坐标以及![]() 确定Q坐标即可;
确定Q坐标即可;
(3)连接DM、DN,由题意可得M、N的坐标分别为(n,![]() ),(n,n),MN=|
),(n,n),MN=|![]() n-2|,然后再分MN=DM,MN=DN,DM=DN三种情况解答即可.
n-2|,然后再分MN=DM,MN=DN,DM=DN三种情况解答即可.
解:(1)∵![]()
∴![]()
![]()
∴![]()
![]()
把![]() 、
、![]() 代入
代入![]() 中,得:
中,得:
![]()
解得: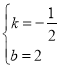
∴![]()
(2)存在点![]() ,使
,使![]() .
.
∵![]()
![]()
∴![]()
![]()
∴![]()
∵![]()
∴![]() 点的纵坐标为0或4
点的纵坐标为0或4
∴![]()
![]()
(3) ①当DM=MN或DM=DN时,如图:过M做DM∥x轴交y轴于D点,连接DN
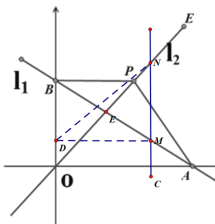
∵C点坐标为(n,n),
∴M、N的坐标分别为(n,![]() ),(n,n),D(0,n) MN=|
),(n,n),D(0,n) MN=|![]() n-2|,
n-2|,
∴|![]() n-2|=|n|,解得:n=4或n=
n-2|=|n|,解得:n=4或n=![]()
②当DM=DN或DM=DN时,如图
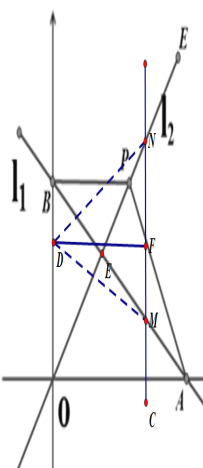
∵C点坐标为(n,n),
∴M、N的坐标分别为(n,![]() ),(n,n),D(0,n) MN=|
),(n,n),D(0,n) MN=|![]() n-2|,
n-2|,
又∵![]() 是等腰直角三角形
是等腰直角三角形
∴D在MN的垂直平分线上,DF=![]() MN
MN
∴,D(0, ![]() +1)F(n,
+1)F(n,![]() |)
|)
∴|n| =![]() |
|![]() n-2|,解得:
n-2|,解得:![]() 或
或![]()
综上,n的取值为4或![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:(1)b2﹣4ac>0;(2)abc>0;(3)8a+c>0;(4)6a+3b+c>0,其中正确的结论的个数是( )
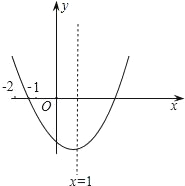
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展我市旅游经济,丹东天桥沟景区对门票采用动态的售票方法吸引游客,规定:门票定价为100元/人,非节假日打
 折售票,节假日按团队人数分段定价售票,即10人以下(含10人)的团队按原价售票;超过10人的团队,其中10人仍按原价售票,超过10人部分的游客打
折售票,节假日按团队人数分段定价售票,即10人以下(含10人)的团队按原价售票;超过10人的团队,其中10人仍按原价售票,超过10人部分的游客打 折售票。设某旅游团人数为
折售票。设某旅游团人数为 人,非节假日购票款为
人,非节假日购票款为 (元),节假日购票款为
(元),节假日购票款为 (元),
(元), 、
、 与
与 之间的函数图象如图所示.
之间的函数图象如图所示.(1)观察图象可知:
 _______,
_______, __________;
__________;(2)直接写出
 和
和 的函数关系式(不需要写出自变量的取值范围);
的函数关系式(不需要写出自变量的取值范围);(3)导游小王10月1日带
 团,10月20日(非节假日)带
团,10月20日(非节假日)带 团都到天桥沟景区旅游,共付门票款4600元,
团都到天桥沟景区旅游,共付门票款4600元, 、
、 两个团队合计60人,求
两个团队合计60人,求 、
、 两个团队各有多少人?
两个团队各有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF; ③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是( )
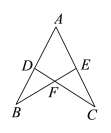
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,CD是∠ACB的平分线, DE垂直平分BC,若DE=2,则AB=___________.
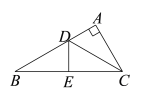
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明与小志要到延庆冬奥综合训练馆参加滑冰训练,他们约定从德胜门出发自驾前往,但他们在选择路线时产生了分歧.根据导航提示小明选择方案1前往,小志选择方案2前往,由于方案1比方案2的路线长,而小明还想大家一起到达.已知小明的平均车速比小志的平均车速每小时快8千米,请你帮助小明算一算,他的平均车速为每小时多少千米,他们就可以同时到达?

相关试题

