【题目】小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
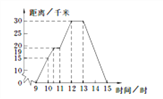
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
参考答案:
【答案】(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看出12:00时他到达离家最远的地方,离家30千米. (4)由图象看出11时距家19千米,12时距家30千米,11时到12时他行驶了30- 19=11(千米). (5)由图象看出12:00~13:00时距离没变且时间较长,得12:00~13:00休息并吃午餐. (6)由图象看出回家时用了2小时,路程是30千米,所以回家的平均速度是30÷2=15(千米/时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
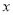 的函数
的函数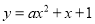 (
(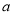 为常数)
为常数)(1)若函数的图象与
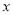 轴恰有一个交点,求
轴恰有一个交点,求 的值;
的值;(2)若函数的图象是抛物线,且顶点始终在
 轴上方,求
轴上方,求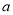 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
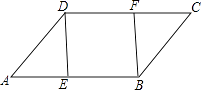
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6
B.2a+3a=6a
C.a2+a2+a2=3a2
D.a2+a2+a2=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、G分别是正方形ABCD的边CD、BC上的点,连接AE、AG分别交对角线BD于点P、Q.若∠EAG=45°,BQ=4,PD=3,则正方形ABCD的边长为( )

A.6
B.7
C.7
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣5>3的解集 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(-7a2+2a-1)﹣2(1-3a2),其中a=﹣1
相关试题

