【题目】如图,点E、G分别是正方形ABCD的边CD、BC上的点,连接AE、AG分别交对角线BD于点P、Q.若∠EAG=45°,BQ=4,PD=3,则正方形ABCD的边长为( ) 
A.6 ![]()
B.7
C.7 ![]()
D.5
参考答案:
【答案】A
【解析】解:如图,延长CB到F,使BF=DE,连接AF,在AF截取AH=AP,连接HQ, 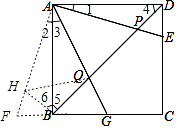
∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠4=∠5=45°,∠BAD=∠ADE=∠ABF=90°,
在Rt△ABF和Rt△ADE中,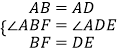
∴Rt△ABF≌Rt△ADE(SAS),
∴∠1=∠2,
∴∠GAF=∠2+∠3=∠1+∠3=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAG,
在△PAQ和△HAQ中,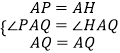
∴△PAQ≌△HAQ(SAS),
∴PQ=HQ,
在△DAP和△BAH中,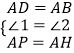 ,
,
∴△DAP≌△BAH(SAS),
∴∠6=∠4=45°,DP=BH=3,
∴∠QBH=∠6+∠5=∠4+∠5=90°
∴BH2+BQ2=32+42=HQ2=PQ2 ,
∴PQ=HQ=5,
∴BD=3+5+4=12,
∵四边形ABCD是正方形,
∴AD=AB= ![]() BD=6
BD=6 ![]() ,
,
故选A.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
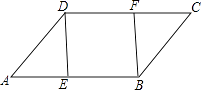
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2a3=a6
B.2a+3a=6a
C.a2+a2+a2=3a2
D.a2+a2+a2=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
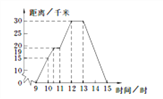
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣5>3的解集 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:(-7a2+2a-1)﹣2(1-3a2),其中a=﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w
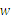 (千克)随销售单价x
(千克)随销售单价x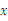 (元/千克)的变化而变化,具体关系式为
(元/千克)的变化而变化,具体关系式为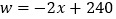 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为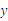 y(元),解答下列问题:
y(元),解答下列问题:(1)求y
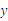 与x
与x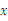 的关系式.
的关系式.(2)当
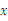 x取何值时,
x取何值时,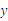 y的值最大?
y的值最大?(3)如果公司想要在这段时间内获得
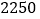 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元?
相关试题

