Question

【题目】如图，在Rt△ABC中，∠C=90°，AB=10cm，AC=8cm．点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s．当一个动点到达终点时，另一个动点也随之停止运动．设运动时间为t（s）．

（1）当t为何值时，△APC为等腰三角形．
（2）当点Q在线段BC上运动时，△PBQ的面积为S（cm2），写出S与t之间的函数关系．
（3）当点Q在线段BC上运动时，是否存在某一时刻t，使S△PBQ：S四边形APQC=5：3？若存在，求出t值；若不存在，说明理由．
（4）在运动过程中，是否存在某一时刻t，使BQ平分∠ABC？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】
（1）解：①当AP=PB时，∵∠ACB=90°，

∴CP=PA=PB，

∴t=5，

②当AC=AP时，t=8，

∴t=5s或8s时，△APC是等腰三角形

（2）解：当点Q在边BC上运动时，过点Q作QH⊥AB于H，

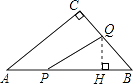
∵AP=xcm，

∴BP=（10﹣x）cm，BQ=2xcm，

∵△QHB∽△ACB，

∴ = ，

∴QH= xcm，

y= BPQH= （10﹣x） x=﹣ x2+8x（0＜x≤3）

（3）解：存在．∵S△PBQ：S四边形APQC=5：3，

∴﹣ x2+8x= × ×6×8，

解得x= 或 ，

∴t= s或 s时，S△PBQ：S四边形APQC=5：3

（4）解：存在．如图作QH⊥AB于H．

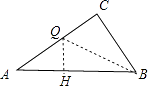
∵∠QBC=∠QBA，QC⊥BC，QH⊥AB，

∴QC=QH=2t﹣6，AQ=14﹣2t，

∵∠A=∠A，∠AHQ=∠C=90°，

∴△AQH∽△ABC，

∴ = ，

∴ = ，

∴t= ，

∴t= s时，BQ平分∠ABC

【解析】（1）分两种情形讨论求解①当AP=PB时，可以证明CP=PA=PB，t=5，．②当AC=AP时；t=5，t=5s或8s时，△APC是等腰三角形
（2）当点Q在边BC上运动时，过点Q作QH⊥AB于H，由△QHB∽△ACB，推出 QHAC=QBAB 可得QH的长度， 根据y= 12 BPQH，列出式子即可；
（3）存在．由S△PBQ：S四边形APQC=5：3，可得关于x的方程，解方程即可解决问题；
（4）存在．如图作QH⊥AB于H．首先得出QC=QH=2t-6，AQ=14﹣2t，由△ AQH∽△ABC，可得 AQAB=QHBC ，从而列出方程， 解方程即可解决问题；
【考点精析】关于本题考查的三角形的面积和相似三角形的判定与性质，需要了解三角形的面积=1/2×底×高；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．